AutoTime Overview
We continue to explore the fusion of LLM and time series. This more recent work reaches new state of art performance on time series forecasting compared to the previous two (TimeLLM and TEST). The repository can be found here . In comparison to previous approaches, the main difference is that AutoTime leverages the autoregressive nature of LLMs, hence it is able to generate predictions of arbitrary lengths. It uses similar patch-based encoding for the time series, but also treats the time stamps text as positional encodings. In the figure below, we can summarize the steps:
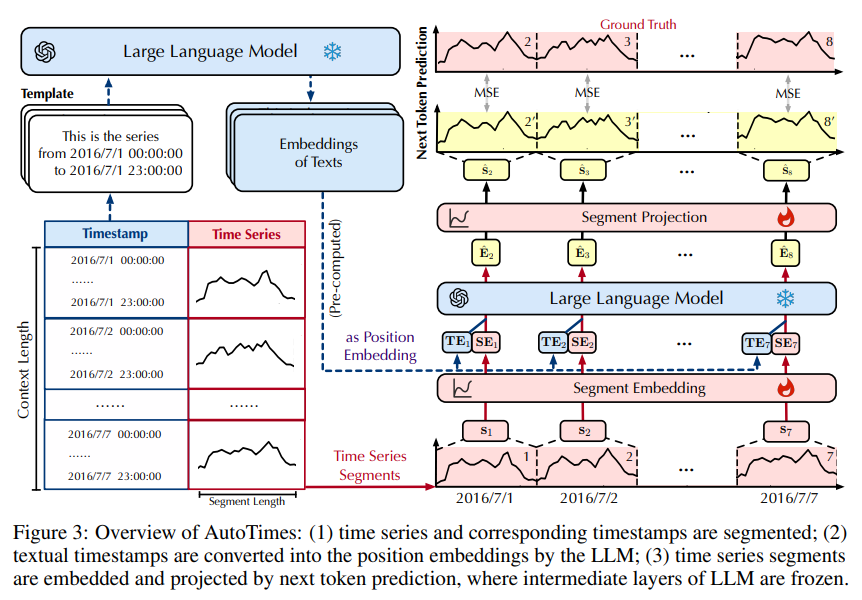
- step 1: The time series data is first divided into small segments, also termed as “patches” ${s_i}$. These patches are then used to generate the time series embeddings. (segment embeddings $SE_i$)
- step 2: The starting and ending timestamps of each segments, as texts, are encoded by a frozen LLM to generate positional embeddings. (positional embeddings $PE_i$)
- step 3: The segment embeddings and the positional embeddings are added together to formulate the token embeddings ($E_i = SE_i + PE_i$) fed into the LLM decoder.
- step 4: LLM decoder generates next step token embeddings based on the input token embeddings:
$$
\begin{aligned}
{\hat{E}_2, \cdots, \hat{E}T} = \text{LLM}({E_1, \cdots, E{T-1}})
\end{aligned} $$ - step 5: The token embeddings are mapped back into time series patches. ${\hat{s}_i}$.
In the end, standard MSE loss is calculated between the predicted time series patches and the ground truth time series patches.
Let’s take a look at the code for each step:
Step 1: Patch Embedding
The steps for patch embedding is almost the same as the TimeLLM paper, where the data loader in data_provider.data_loader.py splits the time series into small segments, and for each segment, it returns the segment (seq_x, seq_y) and the timestamps (seq_x_mark, seq_y_mark).
def __getitem__(self, index):
feat_id = index // self.tot_len
s_begin = index % self.tot_len
s_end = s_begin + self.seq_len
r_begin = s_end - self.label_len
r_end = r_begin + self.label_len + self.pred_len
seq_x = self.data_x[s_begin:s_end, feat_id:feat_id+1]
seq_y = self.data_y[r_begin:r_end, feat_id:feat_id+1]
seq_x_mark = self.data_stamp[s_begin:s_end:self.token_len]
seq_y_mark = self.data_stamp[s_end:r_end:self.token_len]
return seq_x, seq_y, seq_x_mark, seq_y_mark
The embedding of the patches is handled in models.AutoTimes_Llama.py, where similar preprocessing as TimeLLM is applied, and a linear layer (encoder) is used to embed the patches.
# in forecast
means = x_enc.mean(1, keepdim=True).detach()
x_enc = x_enc - means
stdev = torch.sqrt(
torch.var(x_enc, dim=1, keepdim=True, unbiased=False) + 1e-5)
x_enc /= stdev
bs, _, n_vars = x_enc.shape
# x_enc: [bs x nvars x seq_len]
x_enc = x_enc.permute(0, 2, 1)
# x_enc: [bs * nvars x seq_len]
x_enc = x_enc.reshape(x_enc.shape[0] * x_enc.shape[1], -1)
# fold_out: [bs * n_vars x token_num x token_len]
fold_out = x_enc.unfold(dimension=-1, size=self.token_len, step=self.token_len)
token_num = fold_out.shape[1]
# times_embeds: [bs * n_vars x token_num x hidden_dim_of_llama]
times_embeds = self.encoder(fold_out)
here everything is flattned before it is fed into the linear layer.
Step 2: Positional Embedding
The positional embeddings are obtained using Llama encoder on the timestamps, and the code can be found in models.Preprocess_Llama.py:
class Model(nn.Module):
def __init__(self, configs):
super(Model, self).__init__()
self.device = configs.gpu
print(self.device)
self.llama = LlamaForCausalLM.from_pretrained(
configs.llm_ckp_dir,
device_map=self.device,
torch_dtype=torch.float16,
)
self.llama_tokenizer = LlamaTokenizer.from_pretrained(configs.llm_ckp_dir)
self.llama_tokenizer.pad_token = self.llama_tokenizer.eos_token
self.vocab_size = self.llama_tokenizer.vocab_size
self.hidden_dim_of_llama = 4096
for name, param in self.llama.named_parameters():
param.requires_grad = False
def tokenizer(self, x):
output = self.llama_tokenizer(x, return_tensors="pt")['input_ids'].to(self.device)
result = self.llama.get_input_embeddings()(output)
return result
def forecast(self, x_mark_enc):
# x_mark_enc: [bs x T x hidden_dim_of_llama]
x_mark_enc = torch.cat([self.tokenizer(x_mark_enc[i]) for i in range(len(x_mark_enc))], 0)
text_outputs = self.llama.model(inputs_embeds=x_mark_enc)[0]
text_outputs = text_outputs[:, -1, :]
return text_outputs
def forward(self, x_mark_enc):
return self.forecast(x_mark_enc)
a standard transformer encoder is used here.
Step 3: Token Embedding
in the models.AutoTimes_Llama.py, the token embeddings are obtained by adding the segment embeddings and the positional embeddings; there are some intermediate steps in between, such as normalization of both the segment embeddings and the positional embeddings, and a scaling factor.
times_embeds = times_embeds / times_embeds.norm(dim=2, keepdim=True)
x_mark_enc = x_mark_enc / x_mark_enc.norm(dim=2, keepdim=True)
times_embeds = times_embeds + self.add_scale * x_mark_enc
# outputs: [bs * n_vars x token_num x hidden_dim_of_llama]
Step 4: LLM Decoder + Forecast
In the forecast function in models.AutoTimes_Llama.py, the token embeddings are fed into the LLM decoder, and the output is mapped back to the time series patches.
# outputs: [bs * n_vars x token_num x hidden_dim_of_llama]
outputs = self.llama.model(
inputs_embeds=times_embeds)[0]
# dec_out: [bs * n_vars x token_num x token_len]
dec_out = self.decoder(outputs)
dec_out = dec_out.reshape(bs, n_vars, -1)
# dec_out: [bs x token_num * token_len x n_vars]
dec_out = dec_out.permute(0, 2, 1)
dec_out = dec_out * \
(stdev[:, 0, :].unsqueeze(1).repeat(1, token_num * self.token_len, 1))
dec_out = dec_out + \
(means[:, 0, :].unsqueeze(1).repeat(1, token_num * self.token_len, 1))
return dec_out
where denormalization is applied to the output of the decoder, another linear layer.
In-Context Prompting
In AutoTimes, the authors also experimented on a technique called In-Context Forecasting, where the input time series patches are conditioned on a set of historical time series patches. The idea is that the LLM can use the historical time series patches to help with the forecasting of the future time series patches. This is provided using the last_insample_window function in their dataloader class (for the M4 dataset in particular):
def __getitem__(self, index):
insample = np.zeros((self.seq_len, 1))
insample_mask = np.zeros((self.seq_len, 1))
outsample = np.zeros((self.pred_len + self.label_len, 1))
outsample_mask = np.zeros((self.pred_len + self.label_len, 1)) # m4 dataset
sampled_timeseries = self.timeseries[index]
cut_point = np.random.randint(low=max(1, len(sampled_timeseries) - self.window_sampling_limit),
high=len(sampled_timeseries),
size=1)[0]
insample_window = sampled_timeseries[max(0, cut_point - self.seq_len):cut_point]
insample[-len(insample_window):, 0] = insample_window
insample_mask[-len(insample_window):, 0] = 1.0
outsample_window = sampled_timeseries[
cut_point - self.label_len:min(len(sampled_timeseries), cut_point + self.pred_len)]
outsample[:len(outsample_window), 0] = outsample_window
outsample_mask[:len(outsample_window), 0] = 1.0
return insample, outsample, insample_mask, outsample_mask
def last_insample_window(self):
"""
The last window of insample size of all timeseries.
This function does not support batching and does not reshuffle timeseries.
:return: Last insample window of all timeseries. Shape "timeseries, insample size"
"""
insample = np.zeros((len(self.timeseries), self.seq_len))
insample_mask = np.zeros((len(self.timeseries), self.seq_len))
for i, ts in enumerate(self.timeseries):
ts_last_window = ts[-self.seq_len:]
insample[i, -len(ts):] = ts_last_window
insample_mask[i, -len(ts):] = 1.0
return insample, insample_mask
Conclusion
The codebase follows a similar and a very straight-forward approach as TimeLLM, which makes it a lot easier to read than the TEST codebase. It is interesting to see what happens if we try to combine the specific traits of each of the LLM + TS models, since they are somewhat orthogonal to each other, first in the case of embedding time series patches and align the modalities:
- TimeLLM uses muiltiheaded attention to align the patch embeddings with the word embedding matrix of the LLM (only a subset of words).
- TEST uses contrastive learning techniques within the patches and with the word embeddings through some KMeans like clustering approaches.
- AutoTimes uses the positional embeddings of the timestamps as the second modality, and uses a simple linear layer to align the combined patch + timestamp embeddings with the word embeddings of the LLM.
It would be interesting to see how the performance of AutoTimes changes if we replace the simple linear layer with the alignment mechanisms in TimeLLM or TEST.
In addition, for the input to the LLM (prompts), TimeLLM has the most straightforward prompt, which combines the patch embeddings with texts describing the statistics and highlevel information of the time series. Both TimeLLM and TEST uses some sort of prefix embeddings, such as prompts or soft prompts. Here for AutoTimes, only previous time series were used as context window. Again it would be interesting to see how the performance of AutoTimes changes if we replace the context window with thoes prefix embeddings (or enrich AutoTimes with those prefix embeddings).
Throughout the three papers, there is a lack of discussion on the interplay between different univariate time series, as each dimension of the multivariate time series are encoded independently. This is a research direction worth exploring.