Each week, the online notes consist of two parts:
- A distillation of the online lecture materials
- Discussion Slide.
Week 1 Discussion Materials
Lecture one covers the following topics:
- bit manipulation.
- representation of numbers in computers.
These two are quite simple: just need some exercises to master them. Additional stuff:
- use the GDB debugger in VIM: follows from this link .
Discussion Slide
For lab0, the following:
#include <stdio.h>
int ezThreeFourth(int x) {
int threeX = (x << 1) + x; // Multiply x by 3 using bit shifts and addition
int result = threeX >> 2; // Divide by 4 using right shift
if (x < 0) {
result += (threeX & 3) ? -1 : 0;
}
return result;
}
void printInteger(int input, int output) {
printf("input = %d, output = %d\n", input, output);
}
int main()
{
printInteger(11, result1, ezThreeFourth(11));
printInteger(-9, ezThreeFourth(-9));
printInteger(1073741824, ezThreeFourth(1073741824));
}
in VIM, can use command line and run shell scripts or programs using the keystroke Esc-: to enter command mode, then input:
!gcc -o % lab0 && ./lab
which compiles the current opened program using gcc and then execute it. Use
!clear
To clear out the terminal window’s output.
2’s Complement Range and Signs
Several pointers:
for $n$ bits binary representation of numbers, the maximum value of 2’s complement is $2^{n-1}-1$, while the minimum value is $-2^{n-1}$.
In the first case, the sign bit (most significant) is $0$, and the maximum value for 5 bits is $01111$, or $2^4-1 = 15$. The minimum has $1$ as sign bit and the rest zero: $10000$, which is $-16$ (this is obtained by first minus one to get $01111$ then flip all bits to get $10000$).
- For a signed number, the first bit is the sign bit; for unsigned, it only represents positive numbers. The maximum value in this case is $2^n-1$ rather than $2^{n-1}-1$.
- Knowing the range, for binary arithmetic, if overflow happens, usually a modulo $2^n$ is used (4 bit for $5 + 13 = 18$ modulo 16 gives 2).
- shifting operator is equivlent to multiply and dividing by 2’s power.
>>has two versions: logical shift always prepend $0$ on the left, while arithmetic shift always preprend the sign bit currently in place. - when a signed type and an unsigned type appear together in arithemtic, signed is converted to unsigned. Memorization: “larger floating points win; small things become ints; for equal sizes, unsigned wins” (long + shoft -> long; char + unsigned int -> unsigned int; unsigned int + long -> long)
Week 2 Discussion Materials
General Stuff
General concepts:
- Architecture (ISA): parts of a processor design that one needs to understand to write assmebly code.
- Micoarchitecture: Implementation of the architecture (cache size, core frequency)
- Code Forms:
- Machine code is the byte-level programs that processor executes
- Assembly code is a text representation of the machine code.
- Assembly terminologies: CPU (PC, Register, condition) and Memory (code, data, stack)
- Program Counter (PC): address of the next instruction, called “RIP” in x86-64.
- Register file: heavily used program data
- Condition codes: store status information about most recent arithmetic or logical operations; used for conditional branching.
- Memory: byte addressable array; code for used data; stack to support procedures.
- Interactions: (1) CPU uses addresses to lookup in memory (2) memory and CPU share data (3) memory issues CPU instructions.
- From C into Object Code:
gcc -Og p1.c p2.c -o p- Compiler part
gcc -oG -Sto generate assembly programsp1.sp2.s. - Assembler
gccthen generates object files (binary)p1.o,p2.o - In the end, static libraries and linkers together form executable binary file
p; linker takes care of references and static run-time libraries.
- Compiler part
- Assembly code has no aggregate types such as arrays or structures, and are just contiguously allocated bytes in memory.
- Assembly instructions usually are operations of the types:
- register to register
- register to memory
- memory to register
Assembly Programming
Learning this part must be example and practice based, otherwise might as well just read the x86-64 manual. LHS: C code, RHS: assembly code.
Some symbols:
%is used to refer to a register.$is used for immediate values, e.g., constants. 1,2,or 4 bytes.(%)is used for 8 consecutive bytes of memory at some register. e.g.,(%rax)
Example 1: Memory address:
*dest = t; // movq %rax, (%rbx)
Explanation: %rax is the register holding current value. (%rbx) is the memory address of the register %rdx. Here %rdx is the variable dest, and *dest is memory of dest M[%rbx]. This instruction says “store the value hold at %rax register to the memory address of %rbx register”.
temp = 0x4; // movq $0x4, %rax
*p = 147; // movq $-147, (%rax)
temp2 = temp1; // movq %rax, %rdx
*p = temp; // movq %rax, (%rdx)
temp = *p; // movq (%rax), %rdx
Notice that memory-to-memeory cannot be done in one instruction. More complex instructions
movq 8(%rbp), %rdx
Explanation: this one means to move memory value computed by offsetting (add) 8 to the memory address of %rbp to the register %rdx.
0x8 (%rdx) : computes address 0xf000 + 0x8 = 0xf008
(%rdx, %rcx) : computes address (%rdx) + (%rcx)
(%rdx, %rcx, 4) : compute address (%rdx) + 4 * (%rcx)
0x80 (, %rdx, 2) : computes 2 * (%rdx) + 0x80
Example 2: Swap:
long t0 = *xp; // movq (%rdi), %rax
long t1 = *yp; // movq (%rsi), %rdx
*xp = t1; // movq %rdx, (%rdi)
*yp = t0; // movq %rax, (%rsi)
- By default the register %rdi, %rsi has their memory addresses.
- operation 1 and 2 store the memory address of %rdi and %rsi in two new registers. (read-from-memory-write-to-register)
- operatin 3 and 4 write to memory the values stored in the two new registers. (read-from-register-write-to-memory)
Example 3: leaq:
return x*12; // leaq (%rdi, %rdi, 2), %rax
// salq $2, %rax
leaq src, dst can be used to compute addresses without a memory reference and compute arithmetic expressions. First instruction is doing x = x + x * 2 while the second one is x << 2 so a multiplication of 12 in the end. In arithmetic operations addq, subq, imulq, etc. they always have the form instruction src, dst, but the arithmetic operation is usually dst = dst <operation> src. (e.g., subq src, dst is dst = dst - src.)
Example 4: arithmetic:
long t1 = x + y; // leaq (%rdi, %rsi), %rax %rax stores t1
long t2 = z + t1; // addq %rdx, %rax %rax stores t2
long t3 = x + 4;
long t4 = y * 48; // leaq (%rsi,%rsi, 2), %rdx AND salq $4, %rdx, %rdx stores t4
long t5 = t3 + t4; // 4(%rdi, %rdx), %rcx %rcx stores t5
long rval = t2 * t5; // imulq %rcx, %rax
Here the computation at line 3 is handled together with line 5 with the assembly instruction at line 5. imulq src, dst evaluates to dst = dst * src. The value of %rax is changed multiple times throughout.
Example 5: Boolean Comparisons:
Flow control is about conditional statements (if-else, while loop, for loop, switch statements). First there are some single bit register flags:
CF: carry flag for unsigned carry out from most significant bit (unsigned overflow).ZF: zero flag (expression evaluates to zero)SF: sign flag (expression evaluates to negative)OF: overflow flag (two’s complement overflow)
In the below example, setX type instruction is used; this types of instruction usually end with movzbl, which is a 32-bit instruction that sets upper 32-bits to zero.
return x > y; // compq %rsi, $rdi # compare x:y
// setg %al # set when >
// movzbl %al, %eax # zero upper 32bit of %rax
Example 6: Jumps
The family of jumps usually deal with flow controls explicitly, with if-then-else type of structures. Before, the registers holding function input arguments are usually in order: rsi for first, rdi for second.
long absdiff(long x, long y) {
long result;
if (x > y)
result = x - y;
else:
result = y - x;
return result;
}
The assembly code for this type usually have different “blocks/parts”:
absdiff:
cmpq %rsi, %rdi # x:y, rsi holds x, rdi holds y
jle .L4 # jump to L4 if x < y
movq %rdi, %rax # rax now holds value of y
subq %rsi, %rax # rax now holds value of result, result = x - y
ret
.L4:
movq %rsi, %rax # rax now holds value of x
subq %rdi, %rax # rax now holds value of result, result = y - x
ret
Some C-style conditionals are bad, with side effects.
val = Test(x) ? Hard1(x) : Hard2(x); // both values get computed and produces possibly undesirable side effects.
Example 8: while Loops:
With while loop, it is just a matter of having a loop body portion and a conditional check: if condition is satisfied enter or exit the loop.
long result = 0;
do {
result += x & 0x1;
x >>= 1;
} while (x);
return result;
The assembly version, which also looks like the goto version
movl $0, %eax # result = 0
.L2: # loop:
movq %rdi, %rdx
andl $1, %edx
addq %rdx, %rax
shrq %rdi
jne .L2
rep; ret
Example 9: Switch:
Switch statements usually come with a jump table (jtab), each case would jump to a different part
long w = 1;
switch(x) {
// ...
}
return w;
with assembly code, jump table looks like:
.L4
.quad .L8
.quad .L3
.quad .L5
.quad .L7
In the assmebly, could have direct jumps like jmp .L8 or indirect jumps, jmp *.L4(, %rdi, 8), which jumps from start of jump table (.L4) and get target from effective address at .L4 + x*8.
GDB
Week 3 Discussion Materials
Assembly and Stack
on x86-64, stack grows towards lower memory address (towards “top of stack”)
- e.g., top of stack has the lowest memory address. This is where the
%rspregister is at, also known as the stack pointer. - each function has its owns stakc, and the bottom of the stack is known as the frame pointer,
%rbp. - pushq Src: decrement
%rspby 8, so stack grows, and write operand at address given by%rsp. - popq Dest: read value given by
%rspthen increment%rspby 8 (shrink stack), and store value at Dest (must be a register). - call label: a procedure call that:
- first push return address on stack (so we known where to go back to after label returns)
- jump to label
- ret: pop address from stack and jump to address.
Upon a function call, there are two frames, with current stack frame on top of caller stack frame.
- current stack frame has function parameters that are about to be called, local variables, saved register context, and optionally old frame pointer
- caller stack frame has return address (pushed by call instruction) and arguments for this call.
A useful picture taken from Eli Bendersky’s blog post :
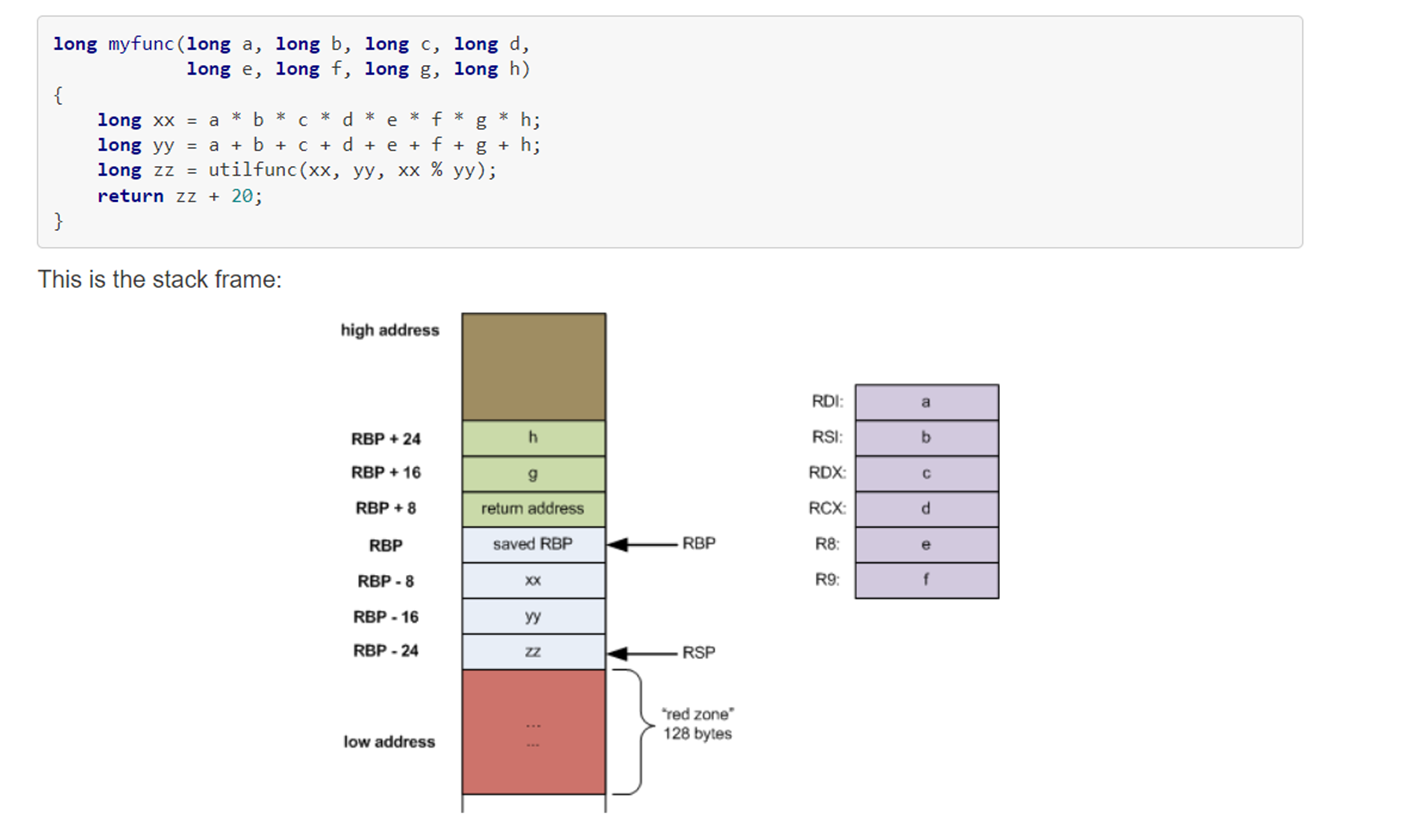
Here the important points are:
- Stack grows to lower memory address and we say it grows from bottom-to-top
%rSPis the stack pointer, pointing to top-of-stack (lowest memory address)%rbpis the base pointer, pointing to bottom-of-stack (highest memory address)- Local storage (between rbp and rsp).
- Additional parameters are stored above rbp.
Regarding push and pop, they are really composite instructions:
For push src, it is equivalent to: grow the stack by subtract 8 from rsp, then move src to the rsp register (top of stack).
subq $8, %rsp
movq src, (%rsp)
For pop dest, it is equivalent to: move to top of stack (%rsp) to dest, then shrink the stack by adding 8 to rsp:
movq (%rsp), dest
addq $8, %rsp
Then for call addr, it pushes the address of the current instruction (%rip) on to the top of the stack then jump to the address, so that when the called function returns, it goes back to the original next instruction, specified by %rip register:
pushq %rip
jmp addr
For ret, it simply pops the top of the stack %rip and resumes to the next instruction from the caller:
popq %rip
Some conceptual stuff: First, about stack frames: these are instantiations of a function during execution, so that everytime a function is called, a new frame is created from callq. Notice that every time this instruction is used, the last thing before the new frame is always the return address of the caller. Frames are then destroyed with a call to retq, with rip (rsp) holding the return address that’s about to be popped. Moreoever:
- A frame holds the local variables for an instantiation of a function.
- The frame is also in charge of holding the values that the callee is responsible for saving. The callee must restore these values before returning to the caller.
- Lastly, if the function is going to make another call, the values that the caller is in charge of saving must also be stored on the frame so that they may be restored after the call returns.
Then, Caller vs Calle: programs can have several functions and each of which are implemented in some way using assembly. Each function is capable of manipulating the stack and they all share a large memory space known as the heap which is great, but there are only 16 registers. Each process must use these registers in order to perform operations on variables and memory, but when a function calls another function, control is passed over to the callee from the caller and the callee starts working with the registers as well We need to decide who is responsible for saving the state of the registers for later use. Registers are divided between caller-responsible and calle-responsible registers:
- Caller responsible registers:
raxfor return value.rdi,rsi,rdx,rcx,r8,r9for function argumentr10,r11for caller-saved temporaries
- Callee responsible registers:
rbx,r12,r13,r14,r15,rbpfor callee-saved temporariesrspas a special register.
Then this week also talked about memory alignment in C, which is basically two rules of thumb:
- For hybrid data structures like
struct, two paddings happen:- if a larger data type follows a smaller data type, padding is added to the smaller type to match the larger type.
- In the very end, the size of the data structure should be a multiple of the largest data type within.
In the end, C arrays are arranged in row-major ordering and are store continuously in memory.
Week 4 Discussion Materials
This week has more fun stuff going on, it is perhaps the first time for most students to put on a black hat. First a more in-depth study about memory layout of a program is studied:
Besides stack, there are also other regions in memory for storage purposes:
- Heap: these regions are dynamically allocated using C function calls such as
malloc(),calloc(), andnew()and when the heap grows, it grows from low address to high address. (opposite to the stack). - In between the region for stack and the region for heap, there’s the shared libraries that are executables and read-only.
- Below the heap (lower memory address), the Data region is used to store statically allocated data such as global variables, static variables, and string constants.
Buffer Overflow
The central idea of buffer overflow attack is, in its most basic form:
overflow the stack memory storage, so as to overwrite rip register to jump to address of injected malicous code.
This means there are some assumptions:
- stack needs to be writable (memory needs to be writable)
- malicious code injected needs to be executable. (stack needs to be executable)
- injected address (which overrides return to
rip) leads to malicious code.
It is most commonly achieved by exceedingly write to arrays (or strings). Old C style functions such as get(), strcpy(), strcat(), scanf, fscanf, sscanf can read from STDIO and write to arrays, which gives lots of potential for stack abuse! From this observation, the first measure to avoid buffer overflow attack is:
- Avoid writing buggy codes, by first avoid using those functions:
fgetsinstead ofgetsstrncpyisntead ofstrcpy.- don’t use
scanfwith%sconvention.
For the assumption 3, randomized stack offsets can help to make it hard for attackers to guess the beginning address of inserted code.
- However, if the system doesn’t randomly change memory, this maybe bypassed by a technique known as fuzzing, which uses probability to search for the address, hence stack is repositioned every time program executes to reduce this chance.
For the assumption 1 & 2, can mark memory regions as non-executable. This however, can be bypassed later on using gadgets chaining and return-to-libC attacks.
Also for assumption 1 & 2, stack canary can be used, which are special values on stack beyond buffer, to check for corruption before exiting function; gcc uses -fstack-protector flag to compile programs with stack canary. Stack canary can even help with the return-to-libC attack.
Return Oriented Programming (ROP)
The most fun attack method at this level is known as return-oriented programming (ROP), which basically builds up attack scripts from gadgets using legitimate library codes. (This is like using Lego parts to build a weapon!):
- gadgets are usually parts of well-defined system codes and ends with
ret. - since these codes are well-defined, their memory addresses are not randomized; moreover, they are executable, and are legitimate so not falling into stack canary check.
Moreoever, this technique can be expanded to perform remote, black-box attack, as seen from the work Hacking Blind , which is one of the forefront work that I found interesting while learning CS33 for the first time, during my undergraduate years.
Second part of this week’s lecture is less fun but necessary:
Floating Points
In Normalized Encoding Example, Floating points from the IEEE convention has the numerical form:
$$ v = (-1)^s M 2^E $$
where $s$ is the sign bit, $M$ is called Significand and usually a fractional value in $[1.0, 2.0)$, and $E$ is exponent that weights value by power of two. Encoding uses (bit count for $s$, exp, frac):
- 1, 8, 23 for single precision 32 bits (C float by default is single precision)
- 1, 11, 52 for double precision 64 bits (C double by default is double precision)
- 1, 15, 64 for extended precision 80 bits
Exponent is coded as biased value: E = Exp - Bias.
- Exp: unsigned value of exp field
- Bias = $2^{k-1}-1$, where $k$ is the number of exponent bits.
Significand coded with implied leading 1: $M = 1.xxx\cdots x$.
Summarizing: $$ v = (-1)^s M 2^E, \quad \text{E = Exp - Bias} $$
Example: float = 15213.0
- $15213_{10} = 11101101101101_2 = 1.1101101101101_2 \times 2^{13}$
- Hence E = 13$
- Significand = $1101101101101_2$
- frac = $11011011011010000000000_2$ (23 bits)
- single precision, 8 bits for exp, so bias = $2^7-1 = 127$.
- Exp = E + Bias = 127 + 13 = 140. Hence we have: $$ \underbrace{0}_{s} \underbrace{10001100}_{exp} \underbrace{11011011011010000000000}_{frac} $$
Denormalized Values: This refers to data with exp = 000…0 $$ v = (-1)^s M 2^E \quad E = 1 - \text{Bias} $$
Special values:
- exp = 000…0, frac = 000…0, this is zero.
- exp = 000…0, frac $\neq$ 000…0, this are numbers closest to zero.
- exp = 111…1, frac = 000…0, this represents infinity and handles overflows.
- exp = 111…1, frac $\neq$ 000..0, this is Not-a-Number (NaN).
Tiny Floating Point: 1 bit sign bit, 4 bits exp, 3 bits frac. In this case, bias = 7, and:
- $v = (-1)^s M 2^E$
- if normalized: E = Exp - Bias
- If denormalized: E = 1 - Bias
Rounding:
Example with rounding: round to nearest 1/4 (2 bits right of binary point).
- $10.00\textcolor{red}{011}_2$, rounded to $10.00_2$, down ($2\frac{3}{32} \rightarrow 2$)
- $10.00\textcolor{red}{110}_2$, rounded to $10.01_2$, up ($2\frac{3}{16} \rightarrow 2\frac{1}{4}$)
- $10.11\textcolor{red}{100}_2$, rounded to $11.00_2$, up ($2\frac{7}{8} \rightarrow 3$)
- $10.10\textcolor{red}{100}_2$, rounded to $10.10_2$, down ($2\frac{5}{8}\rightarrow 2\frac{1}{2}$)
Multiplication rule:
$$ (-1)^{s1} M1 2^{E1} \times (-1)^{s2} M2 2^{E2} = (-1)^{s1\wedge s2} M1\times M2 2^{E1+E2} $$
Fixing:
- if $M \geq 2$, shift M right, increment $E$.
- E out of range, overflow
- Round M to fit frac precision.
Week 5-6 Discussion Materials
Week 6 is midterm week, so these two weeks’ discussion materials are consolidated together.
There are two main topics for this week:
- Memory Hierarchy
- Program Optimization
Program Optimization
As developers, we are mostly familiar with big-O notations, the asymptotic complexity of an algorithm. However, data representations, procedures, and loops can be optimized too. These savings are known as constant factor saving.
First, compilers can be used for optimization, but this optimization is fundamentally constrained due to the lack of behavioral analysis (since compilers only deal with static information). (when in doubt, compilers are conservative)
As programmers, one needs to pay attention to writing optimized codes in terms of execution flows:
- Reduce frequency with which computation performed, if it will always produce the same result; i.e., can move code out of loop.
- In this case, compilers usually cannot automatically provide the necessary optimizations, because compilers treat procedure calls as black box.
- Also, reduce costly operation with simpler ones.
- memory aliasing is a scenario where two memory references specify a single location. Usually you only need to reference the memory once.
On an even lower level, can exploit instruction level parallelism: hardware can execute multiple instructions in parallel; simple transformations can yield dramatic performance improvements. The modern CPU is designed to provide better performance. A superscalar processor can issue and execute multiple instructions in one cycle. These instructions are retrieved from a sequential instruction stream and are usually scheduled dynamically; this allows the instruction level parallelism to be exploited. (since Pentium, Intel CPUs are all superscalar.)
The most important part of this lecture (also heavily in hw and in exam) is the notion of loop unrolling:
- it aims to reduce the number of iterations. i.e., from
i+=1toi+=2within a for loop. This allows reduction of loop overhead and improvement of overall program efficiency. - Especially, if the statements in loop are not dependent on each other, they can be executed in parallel.
- One example is the loop unrolling with re-association:
for (i = 0; i < limit; i+=2) {
x = x OP (d[i] OP d[i+1]);
}
Where the two operations can be executed in parallel. Another approach is called separate accumulators:
for (i = 0; i < limit; i+=2) {
x0 = x0 OP d[i];
x1 = x1 OP d[i+1];
}
Which also achieves parallelism. Overall, loop unrolling has diminishing returns (concave return) so it may not be worthwhile if the statements consist of a large chunk of codes. It also comes at additional memory storage due to the increased code size.
There’s also the efficiency of vector calculation time complexity and optimization. (Advanced Vector Extension) AVX2, also known as Haswell New Instructions is a SIMD (Single Instruction, Multiple Data) extension to the x86 ISA from Intel and AMD. AVX uses 16 YMM registers to perform SIMD, and each register can perform 32-bit single precision or 64-bit double precision floating point operations. SIMD basically ensures better parallelism for floating point operations.
In the end, for branch execution, in order to be efficient, there’s usually a branch prediction that guesses which way branch will go and begins executing instructions at predicted position (without actually modifying registers or memory). Modifications are performed only after the actual branching takes place.
Memory & Storage Hierarchy
RAM (Random-Access-Memory) is traditionally packed as a chip and multiple RAM chips form a memory. There are two types of RAMs:
- Static RAM (SRAM): it has 4-6 transistors per bit, with very fast (1X) access time; doesn’t need refresh, but has high (100X) cost. It is usually used for cache memories.
- Dynamic RAM (DRAM): it has 1 transistor per bit, has (10X) access time, needs refresh and EDC, and has low (1X) cost. It is usually used for main memories, frame buffers. Both are volatile, meaning that information are lost if powered off.
Non-volatile memories are the following:
- Read-only Memory (ROM)
- Programmable ROM (pROM)
- Erasable ROM (EPROM)
- Electrically erasable ROM (EEPROM)
- Flash Memory (EEPROMs with partial erase capability). These are used for Firmware programs, SSDs, Disk caches.
CPU and memory are connected via a bus, a collection of parallel wires that carry address, data, and control signals. Buses are typically shared by multiple devices.
Ex: for a simple assembly instruction of movq %rax, A, multiple steps are involved:
- CPU first places address A on the memory bus.
- Main memory reads A from the memory bus, retrieves word x and places it on the bus.
- CPU read word x from the bus and copies it into register
%rax.
After memory, we then go to disk storage, which are slower but less expensive and contains a lot more content. It has its own controller, the disk controller, and also has its own bus, the I/O bus, that also talks to graphics adaptor, USB controllers, and other I/O devices. To read from a disk, similarly there are multiple steps:
- CPU initiates a disk read by writing a command, logical block number, and destination memory address to a port address associated with the disk controller.
- Disk controller reads the sector and performs a direct memory access (DMA) transfer into main memory.
- When the DMA transfer completes, the disk controller notifies the CPU with an interrupt.
Solid State Disks (SSDs) are nowadays the most popular form of disk storage. It has flash memory, with 32 to 128 pages, each page from 512 KB to 4 KB, with data read/write in units of pages. Details about disk storage and pages are covered in more details in CS 111 (Operating System Principles). In SSD, sequential access and random access modes are both possible, with sequential access faster than random access mode.
Throughout the above steps, we can notice that there’s a gap between CPU and memory.
- CPU to SRAM is the fastest.
- Then CPU to DRAM (10x~100x more time).
- Then CPU to SSD (~$10^5$ more time).
- Then CPU to disk ($\geq 10^7$ more time). This hierarchy is known as memory locality.
Principle of Locality: programs tend to use data and instructions with addresses near or equal to those they have used recently.
- Temporal locality: recently referenced items are likely to be referenced again in the near future.
- Spatial locality: items with nearby addresses tend to be referenced close together in time. (think about C multi-dimensional arrays and indexing)
Another more common word is just caching, which also introduces concepts of memory hierarchy.
The lecture slide provides a good pyramid-like visualization for this hierarchy; in words, this would correspond to, from the faster/smaller/costlier to slower/bigger/cheaper:
- $L_0$: The registers in CPU, which holds word retrieved from $L_1$ cache.
- $L_1$: The SRAM, cache lines retrieved from $L_2$ cache.
- $L_1$ i-cache and d-cache, each 32 KB, 8-way, in Intel Core i7. Access requires 4 cycles.
- $L_2, L_3$: Also SRAM; $L_2$ holds lines retrieved from $L_3$ while $L_3$ retrieves from main memory.
- $L_2, L_3$ are unified caches, $L_2$ is 256 KB, 8 way with 10 cycles to access, while $L_3$ is 8 MB, 16-way, and requires 40-75 cycles to access.
- $L_4$: main memory, the DRAM.
- $L_5$: local secondary storage such as SSD and HDD.
- $L_6$: remote secondary storage such as web servers.
Cache is defined as a smaller, faster storage device that acts as a staging area for a subset of data in a larger, slower device. The big idea is that, memory hierarchy creates a large pool of storage that costs as much as the cheap storage near the bottom, but that serves data to programs at the rate of the fast storage near the top.
- Feasible because of locality.
- Blocks from memory cached: if request from the hierarchy above requests data already in cache, this is a cache hit; otherwise it is a cache miss, and this new entry needs to be cached. A block is 64 bytes.
Cache performance can be measured by:
- Miss rate: fraction of memory references not found in cache, = 1 - hit rate.
- Hit time: time taken to deliver a line in the cache to the processor (this includes the time to deliver a line in the cache to the processor). Typically, 4 block cycles for L1 and 10 cycles for L2.
- Miss Penalty: additional time required because of a miss. (50-200 cycles for main memory)
Missing a cache is massively more expensive (100x) than having the data already in the cache. This is why miss rate is used instead of hit rate. ($97%$ hit translates to $1+0.03\times 100 = 4$ cycles, while $99%$ hit translates to $1+0.01\times 100 = 2$ cycles.)
Therefore, when writing code, it is important to respect the locality principle, make the common case fast, and minimize the misses in the inner loops.
Example: Matrix Multiplication
An very relevant and important example is analyzing locality in matrix multiplication. We know that different algorithms exist for faster matrix multiplication; however, there’s an equally important hardware aspect of performing this operation: different order of indices matter because of locality. The analysis of this type is called miss rate analysis.
Consider the standard, $O(n^3)$ complexity matrix multiplication algorithm between two $n\times n$ matrices. Assume that:
- block size = 32 B
- matrix dimension is very large
- cache is not even big enough to hold multiple rows.
The matrix multiplication operation can be written as index notation, as $C_{ij} = A_{ik}B_{kj}$.
Case 1 (ijk):
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < n; j++)
// a[i][k] is row-wise
// b[k][j] is col-wise
sum += a[i][k] * b[k][j];
}
c[i][j] = sum; // c is constant time
}
If the loop structure is done as:
- Stepping through columns in one row (STCR): e.g, this iterates the multi-dimensional array in a row-wise manner, then the miss rate is $sizeof(A_{ij})/b$, where $b$ is the block size, e.g., depending on size of block.
- Stepping through rows in one column (STRC): since C multidimensional arrays are stored in the row-major form, the miss rate would be $1$! Therefore, for case 1, since the summation is over the index $k$, it is dealing with matrix $A$ in the STCR way but B in STRC way; this definitely can be improved.
Case 2 (jik):
for (j = 0; j < n; j++) {
for (i = 0; i < n; i++)
sum = 0.0;
for (k = 0; k < n; k++)
// a[i][k] is row-wise
// b[k][j] is col-wise
sum += a[i][k] * b[k][j];
}
The only difference is just changing of $i,j$ order; this wouldn’t change the overall performance. The catch is to use the index $k$ wisely: since this is the index for column. We want to iterate through it first to achieve STCR.
case 3 (kij):
for (k = 0; k < n; k++) {
for (i = 0; i < n; i++) {
r = a[i][k]; // a is constant time access
for (j = 0; j < n; j++)
// c[i][j] row-wise
// b[k][j] row-wise (since k is outside)
c[i][j] += r * b[k][j];
}
}
This case we have two STCR, which should be the best case scenario!
case 4 (ikj):
for (i = 0; i < n; i++) {
for (k = 0; k < n; k++) {
r = a[i][k]; // a is constant time access
for (j = 0; j < n; j++)
// c[i][j] row wise
// b[k][j] row wise
c[i][j] += r * b[k][j];
}
}
this is equivalently fast as case 3.
case 5 (jki):
for (j = 0; j < n; j++) {
for (k = 0; k < n; k++) {
r = b[k][j]; // B is constant time
for (i = 0; i < n; i++)
// c[i][j] is col-wise
// a[i][k] is col-wise
c[i][j] += a[i][k] * r;
}
}
As can be seen this is the worst case (both accesses are column-wise).
case 6 (kji):
for (k = 0; k < n; k++) {
for (j = 0; j < n; j++) {
r = b[k][j]; // constant
for (i = 0; i < n; i++)
// c[i][j] is col-wise
// a[i][k] is col-wise
c[i][j] += a[i][k] * r;
}
}
This is also the worst case scenario (both accesses are column-wise).
In addition to this example, the block matrix multiplication leverages the locality principle even better; it was summarized that:
- without blocking, cache miss is of the order $\frac{9}{8}n^3$ while for blocking, it is $\frac{1}{4B}n^3$. Where $B$ is block size.
- Matrix multiplication analysis also has inherent temporal locality, and every array element can be used $O(n)$ times.
The summary from this lecture are that:
- The speed gap between CPU, memory, and mass storage continues to widen.
- Well-written programs exhibit property called locality.
- Memory hierarchies based on caching close the gap by exploiting locality.
- Program writing rule of thumb for efficiency.
- Focus on inner loops, where bulk of computations and memory accesses occur.
- Try to maximize spatial locality by reading data objects with sequentially with stride 1.
- Try to maximize temporal locality by using data objects as often as possible once it’s read from memory.
Week 7 Discussion Materials
This week the focus is on using the openmp library to optimize C codes, based on the tutorial from Tim Mattson at Intel. To consolidate learning on this library, students are assigned the Parallel lab, the last project in the class.
The first high level concept that students need to master is the distinction between parallelism and concurrency. First, regarding the strict definitions:
- Concurrency: a condition of a system in which multiple tasks are logically active at one time.
- Parallelism: a condition of a system in which multiple tasks are actually active at one time.
Concurrency is therefore possible for a single-core machine; actually, only one task is active at a time, but multiple tasks are scheduled and are all running (some waiting, some running). The overall goal of concurrency is to maximize the throughput of a program, e.g., the amount work done per unit of time.
$$ \text{Parallel Programs} \subset \text{Concurrent Programs} $$
Openmp is used to write concurrent programs in C, using compiler directives, enabled using
#include <omp.h>
In the C code and compiled using the gcc -fopenmp flag.
The second important concept is that multiple processes and therefore threads can share the same address space (read and write to the same address spaces); hence if there’s no proper synchronization mechanisms in place, race conditions can happen, resulting in undefined behaviors. This can be tracked using the omp_get_thread_num() call, which identifies the thread calling this function.
OpenMP is a multi-threading, shared address model, where threads communicate by sharing variables; therefore, it requires careful synchronization.
It implements the fork-join parallelism, having a master thread spawning a team of threads. To specify how many threads need to be spawned, use the omp_set_threads(n) function call or the directive # pragma omp parallel num_threads(n) for n threads.
For loop Parallelism
The important example, which appears in homework/exam/project, is how to optimize for loops.
#pragma omp parallel for
// for loop below
#pragma omp parallel for collapse(n)
// for a n-level nested for loop
The loop itself could contain regions where only one thread is allowed to enter at a time. For this case, there are several directives to use (to put before the region with this requirement):
#pragma omp barrier: each thread waits until all threads arrive (usually after some asynchronous calls).#pragma omp critical: defines a critical region where only one thread can enter at a time.#pragma omp atomic: a critical region with only atomic instructions (such as increment, decrement, etc.) and requires less overhead than critical.
Usually, however, it is more natural to use reduction and private, as seen below:
double ave=0.0, A[max]; int i;
#pragma omp parallel for reduction(+:ave)
for (i = 0; i < max; i++){
ave += A[j];
}
ave = ave / max;
Here reduction(+:ave) says that each thread has its own copy of the ave variable, starting from the value of zero for addition later on. After thread finish, local copies are reduced into a single value and combined with the original global value (by addition).
+:has initial value of zero.*:has initial value of one.-:has initial value of zero.
Sometimes we also want to avoid sharing, e.g., each thread has its own local variables; for example, random numbers; this requires using private
double ave=0.0, A[max]; int i;
#pragma omp parallel for reduction(+:ave) private(rand)
for (i = 0; i < max; i++){
int rand = Rand();
ave += A[j] * rand;
}
ave = ave / max;
Or a more useful example, of Monte Carlo Estimation:
#include "omp.h"
static long num_trials = 10000;
int main() {
long i; long Ncirc = 0; double pi, x, y;
double r = 1.0;
seed(0, -r, r);
// x,y are random, Ncric is global
#pragma omp parallel for private(x,y) reduction(+:Ncirc)
for (i = 0; i < num_trails; i++) {
x = random();
y = random();
if ((x*x + y*y) <= r*r) {
Ncric ++;
}
}
pi = 4.0 * ((double) Ncirc / (double)num_trials);
printf("\n %d trials, pi is %f\n", num_trials, pi);
}
In the end, we have the concept of locking, which is covered in a lot more details in CS 111. In CS 33, just need to know that each thread can lock a resource (so other threads cannot use it), using omp_init_lock(ptr) function with a pointer input, to initialize the lock, then omp_set_lock(ptr) to lock it, and omp_unset_lock(ptr) to unlock it (so other threads can use the resource again).
Week 8 Discussion Materials
Week 8 is a prelude to CS 111, Operating System Principles, where the following topics are covered:
- Virtual memory.
- Control Flow at OS level.
- Linking for compilers.
Virtual Memory
VM is a great idea from Computer Science. It:
- uses main memory efficiently (uses DRAM as a cache for parts of a virtual address space.)
Conceptually, VM is an array of N contiguous bytes stored on disk, with contents cached in physical memory (DRAM). The cache blocks in this case are called pages (with size $2^p$ bytes). Because there’s huge penalty of cache miss on DRAM, page sizes are usually large (4 KB to 4 MB). There is then a mapping function that maps memory to pages, known as the page table: an array of page table entries (PTE) that maps virtual pages to physical pages. (cache miss in this case is known as page fault). Locality in this case is again very important.
- Simplifies memory management (Each process gets the same uniform linear address space.)
Each process has its own virtual address space, viewed as a simple linear array (of memory). Mapping function scatters addresses through physical memory (well-chosen mappings can improve locality). This also facilitates linking and loading.
- Isolates address spaces (one process can’t interfere with another’s memory, and use program cannot access kernel information and code.)
This is often achieved with additional permission bits. MMU checks these bits on each memory access.
Address translation:
- Virtual address has space $V = {0, 1, \cdots, N-1}, N = 2^n$.
- Physical address has space $P = {0, 1, \cdots, M-1}, M = 2^m$.
- Address translation is a function: $MAP: V \rightarrow P \cup {\empty}$, where $\emptyset$ is for virtual address not in physical memory (invalid or on disk), where $P = 2^p$ for $p$ the number of pages.
- Address translation requires the page table, which takes a look at the virtual address (VA) and the physical address (PA) into different components:
- VA:
- TLB index.
- TLBT (TLB tag).
- VPO: virtual page offset.
- VPN: virtual page number.
- PA:
- PPO: physical page offset.
- PPN: physical page number.
PPN is obtained by looking up from the page table using VPN; VPO is directly mapped into VPO.
Week 9 Discussion Materials
This week the material covers MIPS and the Parallel Lab.