Week 1
This week, we introduced Fluid Mechanics from a “third grade perspective”. Professor Roper introduced to us fluid mechanics in a lively manner; in the first lecture (referred to as “3rd grade definition”, intended for kids in 3rd grade), he defined fluid as that which takes shape of its container. This definition sounds like one of the natural philosophers from ancient Greece.
This class is about “what makes fluid flow” and “what stops them from flowing”, and we listed the following:
- Weight: related to which are gravity, bouyancy, and temperature.
- Pressure: fluid resisting changes in volume.
- Viscous Force: fluid resisting “sharing”, can be thought of as friction between fluid layers.
- Inertia/Momentum: The tendency to remain in motion.
- Electric Fields and Magnetic field: examples in plasma.
- Visco-elasticity: In materials science and continuum mechanics, viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation.
- surface tension: fluid trying to minimize surface area.
Fluid Mechanics arises to study cases where two or more of the above forces balance with each other; PDE models are then created from the balance laws.
Some of the applications that Marcus presented are quite interesting, mostly from biology, some animals, some fungi (his specialty).
1.1 Continuum Hypothesis of Fluid Mechanics
In this section the fundamental hypothesis of fluid mechanics is introduced; any fluid is made up of particles / molecules. One description of fluid can be a description of location of all the particles and their velocity; this is known as the Lagrangian description but can be difficult because there are too many particles. Instead, traditionally we want to model these particles as field, i.e., continuous vector functions $\underline{v}(\underline{x},t)$ that spans the entire space of interest continuously. This then allows the use of calculus. The continuum hypothesis (CH) makes this formulation possible.
To start, it defines a density field, $\rho(\underline{x},t)$, representing the density surrounding a point in space time $(\underline{x},t)$ where $\underline{x} \in \mathbb{R}^3$ is the spatial coordinate; mathematically this is a box of length $L$ around $\underline{x}$. Suppose we index all the particles in a box by index $i$ and each particle has mass $m_i$, then density is defined to be: $$ \begin{aligned} \rho(\underline{x},t) = \frac{1}{L^3} \sum_{i\in \text{Box}} m_i \end{aligned} $$
This notion of density, however, breaks down if the size $L$ becomes too small. There exists a threshold value $l_{m}$ such that if $L < l_m$, then density would fluctuate rapidly due to microscopic uncertainty. This notion is illustrated in the plot below, obtained from here .
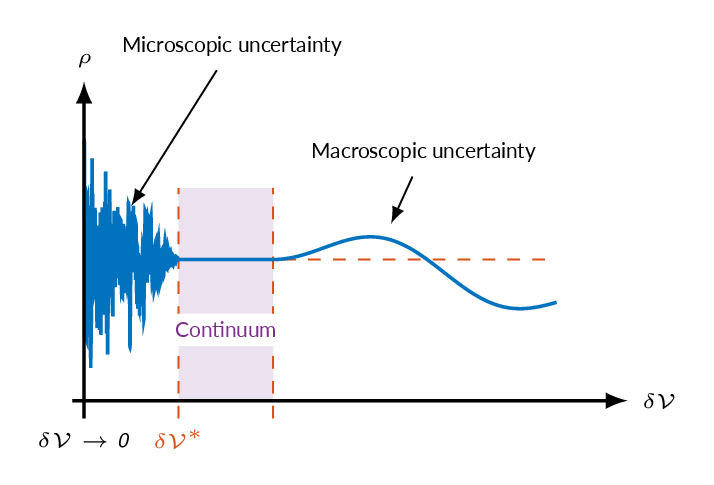
The scale of fluid mechanics therefore doesn’t theoretically go below any $h > 0$ as is customary in calculus, which relies on the infinitesimal: $$ \begin{aligned} \rho(x)’ = \lim_{h\rightarrow 0} \frac{\rho(x+h,t)-\rho(x)}{h} \end{aligned} $$
It has to be greater than $l_m$. How to determine this threshold? This is determined depending on how much fluctuation can be tolerated: suppose that the number of particles is a random variable $N$ that follows a Poisson distribution, $N\sim \text{Poisson}(\mu)$, then the relative fluctuation (RF) is $std(N)/mean(N) \sim \mu^{-1/2}$. Suppose that we want RF < 0.01, then $\mu = 10^4$. Hence we need a box large enough to cover around 10000 particles to have error below this threshold. For liquid, where a particule is around $2-5\times 10^{-10}$ meters, or $0.2-0.5$ nanometers, this means box volume to be between 8 and 125 cubic nanometers. For gas, which is more sparsely distributed in space, this calculation would need to be carried out assuming each pairs of particles have a 20-particle-spacing in between.
The basics of fluid mechanics is to model density $\rho$ (called $C^1$ field) and average velocity $\underline{u}$ (called $C^2$ field), and we define PDEs relating these two quantities using conservalation laws.
The conservation law in this case would be Conservation of Mass, conservation of momentum, and conservation of angular momentum, which will lead to continuity equation and Navier-Stokes Equations.
Conservation of Mass and Continuity Equation
Assume that molecules in a fluid can be moved around but not created or destroyed. Consider a controlled volume $\Omega$ (at this time, assume static volume) with piecewise smooth boundary $\partial \Omega$ that’s oriented (with outward normal vector $\hat{n}$). Then the mass in $\Omega$ is defined as: $$\begin{aligned} M = \int_\Omega \rho(\underline{x},t) dV \end{aligned}$$ At the boundary, there’s also particles moving in and moving out. Since mass is conserved, we must have: $$\frac{dM}{dt} = \int_\Omega \frac{d\rho}{dt}dV = -\int_{\partial\Omega} \rho \underline{u} \cdot \hat{n} dS $$
Where $\underline{u}$ is the velocity field of particle movement. This equation therefore says that the net change of mass in the volume equals the influx/outflux of the particles. In mathematical and physical conventions, the normal vector is outward, so if velocity field is going out, then $dM/dt < 0$, indicating a decrase in mass, confirming our intuition.
By the divergence theorem (or Green’s first identity) we have that: $$ -\int_{\partial \Omega}\rho \underline{u} \cdot \hat{n} dS = -\int_\Omega \nabla \cdot (\rho \underline{u})dV$$
Which holds for any controlled volume, hence we obtain the following: $$ \begin{aligned} \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \underline{u}) = 0 \end{aligned} $$
This results in the continuity equation, which represents the conservation of mass. This equation can be rewritten with material derivative.
Material Derivative
The continuity equation can be rewritten as:
$$\frac{\partial \rho}{\partial t} + \mathbb{u} \cdot \nabla \rho = -\rho (\nabla \cdot \underline{u})$$
where the LHS is usually summarized as $D\rho / Dt$, which is in fact the total derivative of $\rho(\underline{x}(t), t)$. The physical representation of this equation is an observer moving with the fluid located at $\underline{x}(t)$, which measures the density:
$$\begin{aligned} \frac{D\rho}{Dt} &:= \frac{d}{dt} \rho (\underline{x}(t), t) \\ &= \sum_{i=1}^n \frac{\partial \rho}{\partial x_i} \frac{\partial x_i}{\partial t} + \frac{\partial \rho}{\partial t} \\ & \overset{Einstein}{=} \frac{\partial \rho}{\partial x_i} \frac{\partial x_i}{\partial t} + \frac{\partial \rho}{\partial t} \\ & \overset{vector}{=} \frac{d\underline{x}}{dt} \cdot \nabla \rho + \frac{\partial \rho}{\partial t} \end{aligned}$$
usually if $\frac{D\rho}{Dt} = 0$, we have that $\nabla \cdot \rho = 0$, which corresponds to incompressible flow, which physically says “whatever gives the fluid its density flow with $\underline{u}$”.
The next week will start the journey to derive the Navier-Stokes equatins, from conservation of momentum.
Week 2
Conservation of Momentum
First we define Momentum of fluid as:
$$\begin{aligned} M = \int_\Omega \rho \underline{u} dV \end{aligned}$$
In Newtonian mechanics, force acting on $\Omega$ is defined as $\underline{F} = dM/dt$, and for a balance law analysis of the controlled volume $\Omega$, we have that:
$$\frac{d}{dt} \int_\Omega \rho \underline{u} dV = \text{Force on $\Omega$} + \text{rate of inflow of momentum} on \partial \Omega $$
We start with the momentum in flow. Here by convention the direction of pressure on surface is opposite to the outward pointing normal vector $\hat{n}$. For a time interval $\Delta t$, we have that a volume $(\underline{u}\cdot \hat{n})dS \Delta t$ is cleared through the surface element, and the momentum contained in this volume is: $\rho \underline{u} \times (\underline{u}\cdot \hat{n} dS) \Delta t$, or momentum density times volume times time.
And we have that momentum inflow as:
$$\begin{aligned} -\int_{\partial \Omega} \rho \underline{u} (\underline{u}\cdot \hat{n})dS &= -\int_{\partial \Omega} n_i u_i \rho u_j e\above_j dS \\ &=-\int_\Omega \frac{\partial}{\partial x_i}(u_i \rho u_j e_j)dV && \text{Divergence theorem}\\ &=-\int_\Omega \left[\frac{\partial (u_i \rho)}{\partial x_i}u_j e_j + \rho u_i \frac{\partial (u_j e_j)}{\partial x_i}\right] dV \\ &= -\int_\Omega \left[ \nabla \cdot (\rho \underline{u})\underline{u} + \rho \underline{u}\cdot \nabla \underline{u} \right]dV \end{aligned}$$
Now force on $\Omega$ takes two forms:
- Body forces: these are due to fields acting on the matter contained in $\Omega$ and takes form of volume integrals, such as weights: $\int_\Omega \rho g dV$ due to gravity.
- Surface force: these are due to contact with fluid outside $\Omega$, such as fictional viscous force due to flow and pressure force due to volume changes.
Now we present Continuum Hypothesis, Part II:
Each of these forces can be associated with its own “field”.
e.g., pressure force is a scalar field $p(\underline{x},t)$ that measures the amount of normal force acting on $\hat{n}dS$ due to resistance to volume change.
In the absence of viscous forces, conservation of momentum implies:
$$\begin{aligned} \frac{\partial}{\partial t} \int_\Omega \rho \underline{u} dV = -\int_\Omega \left[ \underline{u} \nabla \cdot (\rho \underline{u}) + \rho \underline{u}\cdot \nabla \underline{u} \right] dV + \int_\Omega \rho g dV + \int_{\partial \Omega} -p \nabla dS \end{aligned}$$
where on the RHS, we have the body force and the surface force (pressure). We can further write pressure as $\int_{\partial \Omega} -p\hat{n} dS =-\int_\Omega \nabla \cdot p dV$ by divergence theorem.
Furthermore, we can rearrange the equation above to obtain:
$$\begin{aligned}\underline{u} (\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \underline{u})) + \rho ( \frac{\partial \underline{u}}{\partial t} + \underline{u}\cdot \nabla \underline{u}) = \rho g - \nabla p \end{aligned}$$.
Applying the continuity equation, the first term on LHS is set to zero, and the second term on LHS can be interpreted as the material derivative of $\underline{u}$ multiplied by $\rho$. Hence we arrive at the Euler Equations:
$$\begin{align} & \rho \frac{D\underline{u}}{Dt} = \rho g - \nabla p \\ & \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \underline{u}) = 0 \end{align}$$
Which can be interpreted as unit mass per volume x acceleration = Body force + pressure force; and that fluid accelerates from high pressure regions to low pressure regions. Note that this system of equation has $n+2$ unknowns ($n$ being the dimension of $\underline{u}$) and $(1+n)$ equations, making the well-posedness of famous problem. In this class, we assume that either $\rho$ is a constant (so that $\nabla \cdot \underline{u} = 0$) or that $p = p(\rho)$, which is equation of state.
Hydrostatics
The study of hydrostatics is the study of fluid at rest.
This means $\underline{u} = 0$ and so from the equation above we have $\rho g = \nabla p$, which results in
$$\begin{aligned} p = A - \rho g z \end{aligned}$$ where $z$ is vertical height and A is some constant. If an object is floating and stationary, then its weight must balance the hydrostatic pressure force on its boundary (surface). e.g., weight + hydrostatic pressure force = 0 (the equation above). If the object is not creating any fluid flow, hydrostatic pressure is the same with or without the object; if however, the object is removed and replaced by corresponding fluid flow, then we can apply divergence theorem to the integral:
$$\int_{\partial \Omega} p \hat{n} dS = \int_\Omega \nabla \cdot p dV = \int_\Omega \rho g dV$$
indicating $\rho g = \nabla \cdot p$.
Non-Dimensionalizing
Previously we stated that $\rho$ is a constant, but it may change, due to two reasons:
- $\underline{u}=0$ and boundary is compressing the fluid (this is the case that this course is not considering)
- When $\rho$ changes are caused by the fluid flow (“fast flows”).
For the 2nd case above, to determine “how fast” the fluid flow is, non-dimensionalization analysis can be carried out, which starts by defining scales for terms in the equation:
- $\underline{u} = Uu^{\ast}$, where $u^{\ast}$ is a dimensionless scalar.
- $\rho = \rho_0 + \rho_1$, where $\rho_0$ is the background density and $\rho_1$ the change indensity due to object moving (fast flow). Here assume $\rho_1 « \rho_0$.
- $t = \frac{L}{\underline{u}} t^{\ast}$, where $L/\underline{u}$ is the time taken for object to move its own length, also known as advective time scale.
- $\underline{x} = L\underline{x}^{\ast}$.
Now suppose we temporarily ignore gravity, then the momentum equation is $\rho \frac{D\underline{u}}{Dt} = -\nabla p$; if $\rho$ doesn’t change very much, then we can linearize the equation:
$$p(\rho_0 + \rho_1) \approx p_0 + p’(\rho_0)\rho_1 = p_0 + c^2 \rho_0$$.
Here we have pressure to be of unit $kgs^{-2}m^{-1}$ and $rho$ to be of unit $kgm^{-3}$ and then we have the unit of $p’(\rho_0)$ to be $m^2s^{-2}$, which is square of velocity. Then we can interpret it as speed square, where the speed is the speed of sound.
$$\begin{aligned} \rho_0 (\frac{U^2}{L} \frac{\partial u^{\ast}}{\partial t^{\ast}} + \frac{U^2}{L} \underline{u}^{\ast} \nabla \cdot \underline{u}^{\ast}) = -\frac{C^2}{L}\nabla^{\ast} \rho_1 \end{aligned}$$
For pressure to be of similar size/scale to other terms, it is therefore required that:
$$\rho_1 = \rho_0 \frac{U^2}{L^2} \rho_1^{\ast}$$
Plugging into equation then we obtain that:
$$\nabla^{\ast} \cdot \underline{u}^{\ast} = \frac{U^2}{C^2}\frac{D\rho_1^{\ast}}{Dt^{\ast}}$$
Hence $\nabla^{\ast} \cdot \underline{u}^{\ast} = 0$ if $Ma = \frac{U^2}{C^2} « 1$, which is known as the Mach Number. If this condition holds (which says that speed of fluid flow is much less than the speed of sound) then we have incompressible flows; otherwise we switch to compressible fluid dynamics.
Week 3
Vorticity Equation
Week 3 starts with another analysis of pressure field: pressure is the force field created due to fluid flow changing in density. The Euler’s equation has differential-algebraic structure. A practical question is how to represent solution $\underline{u}$. This usually involves streamlines, which for steady fluid flow, is always perpendicular to the velocity field of the fluid flow.
Formally, a streamline is a curve that is instantaneously tangent to the fluid velocity throughout the flow field.
If $d\underlin{s} = (dx, dy, dz)$ is the Cartesian element of arc length along a strealine and $\underline{u} = (u,v,w)$ is the local velocity field, then:
$$ \frac{dx}{u} = \frac{dy}{v} = \frac{dz}{w} $$
and $\underline{u}\times d\underline{s} = 0$.
If we know the streamlines, we can extract pressure field from Bernoulli’s Principle.
$$\begin{aligned} \rho \underline{u} \nabla \underline{u} = -\nabla p + {\rho g, \underline{F}} \end{aligned}$$
- A lot of body force are conservative, meaning that they can be derived from potentials: $\underline{F} = -\nabla \chi$ for some scalar field $\chi$. For gravity we have $\chi = \rho g z$. This makes the above equation into:
$$\rho \underline{u}\nabla \underline{u} = -\nabla p - \nabla \chi$$
Now the question is: How do $\rho, \underline{u}$ vary on streamlines? It turns out that, from Bernoulli’s principle, we have that:
$$\begin{aligned} \underline{u} \cdot \nabla \underbrace{(\frac{1}{2} \rho \underline{u}\cdot \underline{u} + p + \chi)}_{H \text{(total head)}} = 0 \end{aligned}$$
This is a statement of conservation of energy (but slightly different). Bernoulli’s principle says that $H$ is conserved on streamlines. Now for boundary conditions:
- our boundary maybe solid/rigid. In this case solid boundary moving at velocity $\underline{u}$ then $\underline{u}\cdot \hat{n} = \underline{u} \cdot \hat{n}$.
- open/free boundary on which $p$ is specified.
For the second case, we start with the introduction of the concept of Vorticity:
$$\begin{aligned} \nabla \times (\nabla p) = e_i \epsilon_{ijk} \frac{\partial}{\partial x_j} (\frac{\partial p}{\partial x_k}) \end{aligned}$$
where $\epsilon_{ijk}$ is the permutation tensor ($1$ if permutation, $-1$ if anti-permutation, $0$ otherwise).
Observation: $\nabla \times (\nabla p) = 0$, or that the curl of gradient of vector is zero.
To see this, we have:
$$\begin{aligned} \nabla \times (\nabla p) &= e_i \epsilon_{ijk} \frac{\partial}{\partial x_j} (\frac{\partial p}{\partial x_k}) \\ &= e_i \epsilon_{ikj}\frac{\partial^2 p}{\partial x_k \partial x_j} \\ &= -e_i\epsilon_{ijk}\frac{\partial^2 p}{\partial x_j \partial_k} \\ &= -\nabla \times (\nabla p) \end{aligned}$$
Hence $\nabla \times (\nabla p) = 0$.
At this point, the manipulation of the index notation becomes crucial for derivations. From Euler’s equation for incompressible flow, e.g.,
$$\rho (\frac{\partial \underline{u}}{\partial t} + \underline{u}\cdot \nabla \underline{u}) = - \nabla (p + \chi)$$
we rewrite it in terms of $w$ to derive an equation for vorticity; by directly computing curl, we want to show:
$$\rho (\frac{\partial w}{\partial t} + \nabla \times (\underline{u}\cdot \nabla) \underline{u}) = 0$$
Recall for any vector, $\underline{a},\underline{b},\underline{c}$, we have that:
$$\underline{a}\times (\underline{b} \times \underline{c}) = (\underline{a}\cdot \underline{c})\cdot \underline{b} - (\underline{a}\cdot \underline{b})\cdot \underline{c}$$
which in the index notation is equivalent to (looking only at ith component):
$$\epsilon_{ijk} a_j \epsilon_{klm} b_lc_m = a_jc_jb_i - a_jb_j c_i$$
Here we used the following identities for index notation conversion:
$$\underline{a}\times \underline{b} = e_i \epsilon_{ijk} a_j b_k$$
$$ (\underline{a} \cdot \underline{b})\cdot \underline{c} = a_j b_j c_i$$
$$ \underline{a} \cdot (\underline{b} \cdot \underline{c}) = a_j b_i c_i$$
$$\underline{a}\times (\underline{b} \times \underline{c}) = \epsilon_{ijk} a_j (b \times c)_k = \epsilon_{ijk} a_j \epsilon_{klm} b_l c_m$$
Re-arrange the index for the result above, we can obtain:
$$\epsilon_{kij} \epsilon_{klm} a_j b_l c_m = a_j b_l c_m (\delta_{ij}\delta_{il} - \delta_{jl}\delta_{im})$$
where the Kronecker delta $\delta_{ij} a_j = a_i$, e.g., convert the indices. Since this hold for arbitrary $\underline{a},\underline{b},\underline{c}$, we have the following identity:
$$\begin{align} \epsilon_{kij}\epsilon_{klm} = \delta_{il}\delta_{jm} - \delta_{im}\delta_{jl} \end{align}$$
Since $\underline{u}\times \underline{w} = \underline{u} \times \nabla \times \underline{u}$, we have that:
$$\underline{u} \times \underline{w} = e_i \epsilon_{kij} \epsilon_{klm} u_j \partial_l u_m$$
taking i-th component, we have:
$$ = (\delta_{il}\delta_{jm} - \delta_{im}\delta_{jl}) u_j \partial_l u_m$$
$$ = u_j \partial_i u_j - u_j \partial_j u_i$$
Hence:
$$\begin{align} \underline{u} \times \underline{w} = \nabla \cdot (\frac{1}{2} \underline{u}^2) - (\underline{u}\cdot \nabla) \cdot \underline{u} \end{align}$$
using the above to rewrite $\nabla \times (\underline{u}\cdot \nabla)\cdot \underline{u}$ and plug into Euler’s equation, (and after some tedious calculations), we arrive at the following:
$$\begin{aligned} \nabla \times (\underline{u}\times \underline{w}) = (\underline{w}\cdot \nabla)\underline{u} + \underline{u} (\nabla \cdot \underline{w}) - \underline{w}\cdot (\nabla \cdot \underline{u}) - (\underline{u}\cdot \nabla)\cdot \underline{w} \end{aligned}$$
where we used $\nabla \cdot \underline{w} = \nabla \cdot (\nabla \times \underline{u}) = 0$ and that $\nabla \cdot \underline{u} = 0$. This gives the Vorticity equation:
$$\begin{equation} \frac{D\underline{w}}{Dt} = \frac{\partial \underline{w}}{\partial t} + (\underline{u}\cdot \nabla)\cdot \underline{w} = (\underline{w}\cdot \nabla)\cdot \underline{u} \end{equation}$$
Observe that for this equation:
- if $\underline{w} = 0$ at initial state, then it remains zero.
- It transports (moves around) vortex lines (lines tangent to $\underline{w}$), which follows material points; this allows interpolation based on observed moving particles.
- Vorticity can’t be created.
Moreover, $\nabla \times \underline{u} = 0$ implies there exists a scalar potential $\phi$ such that $\underline{u} = \nabla \phi$. Since $\nabla \times \underline{u} = 0$, we have that $\Delta \phi = 0$, or that $\phi$ satisfies the Laplace’s equation, with Neumann boundary conditions.
Viscous Force and Stress Tensor
Now, having an understanding of vorticity, we proceed to study another form of surface force, called viscous force, in the conservation of momentum. To this end we start with the stress on surface element $\hat{n}dS$, $\underline{T}(\underline{x}, t, \hat{n})$, which has unit of force per area. The key modeling statement is that $\underline{T}$ can be replaced by a tensor field.
A vector field associated with each $(\underline{x}, t)$ a vector; a rank-2 tensor field associate with each $(\underline{x}, t)$ a matrix $\underline{\underline{\sigma}}$
$$\begin{aligned} \underline{T}(\underline{x}, t, \hat{n}) \equiv \hat{n}\cdot \underline{\underline{\sigma}}(\underline{x}, t) \end{aligned}$$
Notice that $\underline{x}$ is a vector, $\underline{\underline{x}}$ is a rank-2 tensor. The introduction of this new viscous force makes our force balance equation to be:
$$\begin{aligned} \frac{d}{dt}\int_\Omega \rho \underline{u} dV + \int_\Omega \nabla \cdot (\rho \underline{u}\underline{u}) dV = \int_\Omega \underline{F}dV + \int_{\partial \Omega} \underline{T} dS \end{aligned}$$
and $\underline{T}$ can be derived from the stress tensor field $\underline{\underline{\sigma}}$ acting on $\partial \Omega$, e.g., $\underline{T} = \hat{n}\cdot \underline{\underline{\sigma}}$, or $T_i = n_j \sigma_{jl}$.
The diea that $\underline{I}$ is derived from $\underline{\underline{\sigma}}$ can be seen from the Cauchy stress tetrahedron.
If the diameter of the tetrahedron is $L$, then we have that:
$$ \text{mass} \times \text{acceleration} = \text{surface force} + \text{body forces} $$
Where mass is of order $O(L^3)$, surface force $O(L^2)$, and body force $O(L^3)$. As $L\rightarrow 0$, we obtain a dominant balance (DB) and sum of surface forces is zero. Let $dA$ be the area of the sloping surface, and let $dA_x$ be the area of $dA$ projected on the $yz$ plane, then we have:
$$ \underline{T}(0, \hat{n}) dS + \underline{T}(0, -\hat{x})dS_x + \underline{T} (0, -\hat{y})dS_y + \underline{T}(0, -\hat{z})dS_z $$
where $\underline{T}(0, \hat{x})$ is the force from fluid on the negative side of the plane with fluid on the side, and by Newton’s 3rd law, we have that: $\underline{T}(0, \hat{x}) = -\underline{T}(0,-\hat{x})$. Moreover,
$$ \underline{T}(\hat{n}) = \underline{T}(\hat{x})\hat{x}_n + \underline{T}(\hat{y})\hat{n}_y + \underline{T}(\hat{z})\hat{n}_z $$
In the force balance equation, we further look at the surface integral:
$$\begin{aligned} \int_{\partial \Omega} \underline{\underline{\sigma}} \hat{n}dS = \int_\Omega \nabla \cdot \underline{\underline{\sigma}} dV \end{aligned}$$
Hence we rewrite the balance equation as the Cauchy Equation:
$$\begin{align} \rho \frac{D \underline{u}}{Dt} = \underline{F} + \nabla \cdot \underline{\underline{\sigma}} \end{align}$$
For a fluid, usually we can explicitly express the tensor field as $\underline{\underline{\sigma}} = -p \underline{\underline{1}} + \underline{\underline{\tau}}$, where we have both an identity tensor and a viscous stress tensor. The intuition is that viscous stresses arise when we have gradients in velocity, e.g., $\underline{\underline{\tau}}$ depends on $\nabla \underline{u}$, which is a Jacobian matrix, $(\nabla \underline{u})_{ij} = \frac{\partial u_i}{\partial x_j}$.
Claim: viscous stress tensor $\underline{\underline{\tau}}$ depends only on the non-rigid body rotation part of $\nabla \underline{u}$, where we perform the decomposition on the jacobian as:
$$\begin{aligned}\nabla \underline{u} = \underbrace{\frac{1}{2}(\nabla \underline{u} + (\nabla \underline{u})^T)}_{\text{non-rigid rotation part } \underline{\underline{E}}} + \underbrace{\frac{1}{2}(\nabla \underline{u} - (\nabla \underline{u})^T)}_{\text{rigid rotation part} \underline{\underline{A}}} \end{aligned}$$
There’s a physical interpretation of this decomposition, and $\underline{E}$ has a special name of strain rate tensor. The strain rate tensor expresses the rate at which the mean velocity changes in the medium as one moves away from the point p – except for the changes due to rotation of the medium about p as a rigid body, which do not change the relative distances of the particles and only contribute to the rotational part of the viscous stress via the rotation of the individual particles themselves (from Wikipedia).
Week 4
Derive the Incompressible Navier Stokes Equation
After the decomposition, we can now write $\underline{\underline{\tau}} \approx \underline{\underline{E}}$, and in particular, $\underline{\underline{\tau}} = 2\mu \cdot \underline{\underline{E}}$, with $\mu$ viscosity, summarizing:
$$ \underline{\underline{\tau}} = \mu (\nabla \underline{u} + (\nabla \underline{u})^T) = 2\mu \underline{\underline{E}} $$
Local flow field can now be represented as: $\underline{u} = \underline{x}\cdot \underline{\underline{E}}$, or equivalently, $u_i = x_j E_{ji} = E_{ij}x_j$. $\underline{\underline{E}}$ being symmetric means it is diagonalizable with the right coordinate system, and we can write:
$$ \text{trace}(\underline{\underline{E}}) = \frac{1}{2}\text{tr}(\partial_i u_j + \partial_j u_i) = \frac{1}{2} (\partial_i u_i + \partial_i u_i) = \partial_i u_i = \nabla \cdot \underline{u} \underbrace{=}_{\text{incompressible}} 0 $$
Plugging this result into Cauchy’s equation and analyze the divergence term $\nabla \cdot \underline{\underline{\sigma}}$, where the viscosity stress tensor satisfies:
$$ \underline{\underline{\sigma}} = -p \underline{\underline{1}} + \mu (\nabla \underline{u} + (\nabla \underline{u})^T) $$
In the index notation, this is (using $\nabla \underline{u} \equiv \partial_i u_j$):
$$ \sigma_{ij} = -p \delta_{ij} + \mu (\partial_i u_j + \partial_j u_i) $$
we compute its divergence using the index notation $\nabla \cdot u = \partial_i u_i$
$$\begin{aligned} (\nabla \cdot \underline{\underline{\sigma}})_{i} = \partial_j \sigma_{ji} = \partial_i \sigma_{ij} = -\partial_i p + \mu (\partial_i \partial_j u_j + \partial_j \partial_j u_i) \end{aligned}$$
Back to vector form, this means:
$$\begin{aligned} \nabla \cdot \underline{\underline{\sigma}} &= -\nabla p + \mu (\nabla (\nabla \cdot \underline{u}) + \nabla^2 \underline{u}) \ &= -\nabla p + \mu \nabla^2 \underline{u} \end{aligned}$$
Concluding, we obtain the Incompressible Navier Stokes equation:
$$\begin{align} \rho \frac{D\underline{u}}{Dt} = -\nabla p + \mu \nabla^2 \underline{u} + \underline{F} \end{align}$$
Concepts from the Navier Stokes Equation
Note 1: The Couette Flow is a toy example, where the profile is created between two parallel planes when one plane is stationary and the other moves tangentially at steady velocity $u$. Physically, viscosity is the friction between fluid and solid molecules, and the velocity field at either plate matches the plate velocity. From this toy case, only one of the velocity component is nontrivial. The NS equation in this toy example reduces to:
$$ \frac{d^2 \underline{u}}{dy^2} = 0, u(0) = 0, u(h) = U $$
with exact solution $u(y) = U\frac{y}{h}$.
The Reynolds Number
The Reynolds number can be used to consider fluid flow in different settings, with varying importance for pressure and viscosity, and it is obtained through the analysis known as Dominant Balance. Consider again the Incompressible Navier stokes equation:
$$ \rho \frac{\partial \underline{u}}{\partial t} + \rho \underline{u} \cdot \nabla \underline{u} = -\nabla p + \mu \nabla^2 \underline{u} + \underline{F}, \nabla \cdot \underline{u} = 0 $$
With non-dimensionalization, we have:
$$ \underline{u} = U \underline{u}^{\ast}, \quad t = \frac{L}{U} t^{\ast}, \quad \underline{x} = L \underline{x}^{\ast} $$
First we need to find the scaling for $p$; from Euler’s equation, $\nabla p \sim \rho \frac{D\underline{u}}{Dt}$; consider $p \sim P p^{\ast}$ then:
$$ \frac{p}{L} \nabla^{\ast} p^{\ast} \sim \rho \frac{U^2}{L} \frac{D \underline{u}^{\ast}}{Dt^{\ast}} \Longrightarrow p \sim \rho U^2 $$
Conversely, if $\mu \nabla^2 \underline{u}$, the viscous force, is dominant, then: $\nabla p \sim \mu \nabla^2 \underline{u}$, then:
$$ \frac{p}{L} \nabla^{\ast} p^{\ast} \sim \frac{\mu U}{L^2} (\nabla^{\ast})^2 \underline{u}^{\ast} \Longrightarrow p \sim \frac{\mu U}{L} $$
If that’s the case and the viscous force is dominant, then ignoring the body force $\underline{F}$ (or saying that it is absorbed in the pressure term), we have:
$$\begin{align} \underbrace{\left( \rho \frac{UL}{\mu} \right)}_{\text{Renolds Number}} \frac{D\underline{u}^{\ast}}{Dt^{\ast}} = -\nabla^{\ast} p + (\nabla^{\ast})^2 \underline{u}^{\ast} \end{align}$$
where we call the first scaling term the Reynolds Number (Re). It is a dimensionless group that expresses how important the inertia is compared with viscous forces. For example, a person swimming has around $10^6$ and airplane has $10^8$ Re. Rewriting the Reynolds number as $Re = \frac{UL}{\mathit{v}}$, where $\mathit{v} = \mu / \rho$ is called the kinetic viscosity; for air, this value is about $10^{-5} m^2s^{-1}$ and for water this is $10^{-6} m^1s^{-1}$, and Viscous force becomes dominant when $UL$ is small (and inertia is dominant), such as in the following scenarios:
- swimming of microorganism.
- intracellular flows.
- microfluid device.
If $Re < < 1$, then we have the Stokes equation:
$$\begin{align} 0 = -\mu \nabla^2 \underline{u} - \nabla p + \underline{F}, \quad \nabla p = 0 \end{align}$$
When $Re > > 1$, this usually refers to tubulence, boundary layers, Euler’s equation, etc. with lots of recent developments in math and many open problems.
Rectilinear Flow
The rectilinear flow has unidirectional streamline and $\underline{u}$ can only vary perpendicular to the streamline. This means automatically $\nabla \underline{u} = 0$ and $(\underline{u} \cdot \nabla)\underline{u} = 0$. Now ignoring $F$ and take a look at the Stokes equation, we have:
$$\begin{aligned} 0 = -\nabla p + \mu \nabla^2 \underline{u} \Longleftrightarrow 0 = \underbrace{-\frac{dp}{dz}}_{G \in \mathbb{R}, \text{function of }z} + \underbrace{\mu (\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}) \underline{u}}_{\text{function only of }x,y} \end{aligned}$$
First term is a function of $z$ only, and the second term is a function of $x,y$ only, hence both are constants. This results in:
$$\begin{align} -\frac{G}{\mu} = \nabla^2 \underline{u}, \quad \text{Poisson’s Equation} \end{align}$$
which assumes analytical solution and is also known as cylinder flow.
$$ \underline{u} = \frac{G}{4\mu} (a^2-r^2) $$
$$ \text{total flow} = 2\pi \int_0^a r u dr = \underbrace{\frac{G \pi a^4}{8\mu}}_{\text{Hagen-Poiseulle law}, \mathcal{Q}} = \frac{\Delta p \pi a^4}{8\mu L} $$
where $\frac{\Delta p}{L} = G$ is the pressure drop per unit length. Total force on cylinder is then $\Delta p \pi a^2$, which balances with the surface force (drag force on the surface of the pipe); if this shear stress at pipe walls is $\tau$, then:
$$ \tau 2\pi a L = \Delta p \pi a^2 \Longrightarrow \underbrace{\tau}_{\text{shear stress}} = \frac{\Delta p a}{2L} = \frac{8\mu \mathcal{Q}}{2a^3\pi} $$
Energetics:
$$ \text{work done by the pressure force in unit time} = \Delta p \int \underline{u} dA = \Delta p \mathcal{Q} = \frac{8\mu L}{\pi a^2}\mathcal{Q} $$
This work being done has to equal to the dissipation of energy (conversion of mechanical energy into heat by viscous force) and was studied by Hooke during his honeymoon in Switzerland.
This has application to: “what is the proper radius of a blood vessel? Mathematically, what value of $a$ optimizes the total energy needed for a vessel? (blood flow is not Newtonian, even though we are treating it as such) Using the above result, this would simply translate to larger $a$, but this is clearly not true, so one way to model it is by adding a cost to building the vessel. Aagin, for the total work done, we call it $\Theta$:
$$ \Theta = \frac{8 \mu L \mathcal{Q}^2}{ \pi a^2} + \underbrace{C \pi a^2 L}_{\text{cost of upkeep of the vessel}} $$
For some unknown constant $C$. simplifying it as $\Theta = c_1 \frac{\mathcal{Q}^2}{a^2} + c_2 a^2$ to see the tradeoff in surface area. This results in the optimal choice of $a$ to be:
$$ \hat{a} = \left( \frac{16\mu}{\pi^2 C} \right)^{1/6} \mathcal{Q}^{1/3} $$
The pre-fractor is hard to measure directly since $C$ is unknown, but the implication that $a\propto \mathcal{Q}^{1/3}$ is testable. It is not always possible to measure $\mathcal{Q}$ in real biological transport networks; in this case, we can test the optimization in a different form. Lock at where vessels and divide a vessel radius into a smaller vessels of radius $a_1,a_2$ and label the flows $\mathcal{Q},\mathcal{Q}_1, \mathcal{Q}_2$, respectively, such that $\mathcal{Q} = \mathcal{Q}_1 + \mathcal{Q}_2$. Then if all vessels obey the optimization principle:
$$ \left( \frac{16\mu}{\pi^2 C} \right)^{1/2} a^3 = \left( \frac{16\mu}{\pi^2 C} \right)^{1/2} a_1^3 + \left( \frac{16\mu}{\pi^2 C} \right)^{1/2} a_2^3 $$
which indicates $a^3 = a_1^3 + a_2^3$. This result is known as Murray’s Law and it can be tested with knowledge only of vessel radii, not of their flows.