Similar to the previous post, I will analyze the source code of the Text Prototype Aligned Embedding for Time Series. The repository can be found here . The main idea of this paper is very similar from TimeLLM, which is to integrate temporal information into the LLM training process. The difference is how the alignment between text and time series is established. Like in the previous post, TimeLLM , I will first analyze the input data and the overall forward pass architecture. However, since the overall flow is very similar, I’ll highlight the differences.
Patching and Contrastive Learning
Similar to TimeLLM, the input data consists of text and time series data. The text data is used to generate the text embeddings, and the time series data is used to generate the time series embeddings. The time series data is divided into small segments, also termed as “patches”. These patches are then used to generate the time series embeddings. The way to generate the time series embeddings is different from TimeLLM, and TEST uses contrastive learning. In specific, for each patch, it generates a positive patch and a negative patch. The positive patch is current patch undergoing augmentations, and the negative patch is an non-overlapping patch from the same time series. The perform the task of embedding, they consutrct an encoder and a decoder, with a reconstruction loss to train the encoder; this encoder is designed as a temporal encoder based on Causal CNN, in the code encoders.causalcnn.py. The core component of this encoder is the truncation of the convolution, which makes the model causal and invariant to the length of the time series.
# in CausalConvolutionBlock
# one layer of causal convolution
# Computes left padding so that the applied convolutions are causal
padding = (kernel_size - 1) * dilation
# First causal convolution
conv1 = torch.nn.utils.weight_norm(torch.nn.Conv1d(
in_channels, out_channels, kernel_size,
padding=padding, dilation=dilation
))
# The truncation makes the convolution causal
chomp1 = Chomp1d(padding)
# chomp1 is a truncation function that removes the padding from the convolution
# forward pass for Chomp1d
return x[:, :, :-self.chomp_size]
To make the contrastive learning more effective, they proposed three different perspectives of contrastive learning, where the overview was in Figure 1 of the paper:
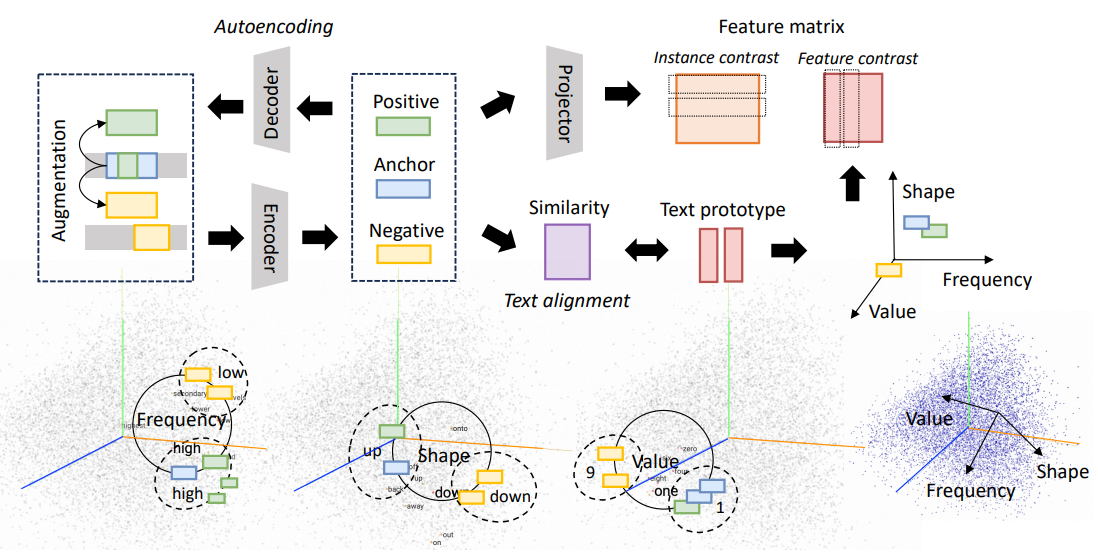
Instance Perspective Contrastive Learning
This perspective treats each patch independently, just like how contrastive learning is applied in the most standard way. They avoid the problem of embedding space collapse by using all other patches in the same minibatch as negative samples. Here a projection head $f_p$ is used to project the patch embedding to a contrastive embedding space (equation 1 in the paper):
$$ \begin{aligned} & \mathcal{L}{ins} = -\log \frac{\exp(\sigma(e,e^+))}{\exp(\sigma(e,e^+)) + \sum{i=1}^B \exp(\sigma(e,e^-))} \\ & \sigma(e,e^+) = \frac{sim(f_p(e),f_p(e^+))}{\tau} \end{aligned} $$
Feature-wise Contrastive Learning
After the instance embedding, for the resulting feature matrix of a minibatch, they use the columns as soft labels for features and performs discriminination between groups of similar features. In practice, they ensure try to ensure difference between features. For a feature matrix $m\in \mathbb{R}^{B]times N}$ each feature/anchor (column) is $m_i$, and the positive feature matrix is $m^+$, the negative feature matrix is $m^-$. The following loss function is used:
$$ \begin{aligned} \mathcal{L}{fea} = -\sum{i=1}^M (\sigma(m_i,m^+) - \sigma(m_i,m^-)) \end{ailgned} $$
Text-prototype Contrastive Learning
This is the part where they align the embedding spaces of text and time series patches. Given the word embedding matrix of a LLM, they choose $P$ representative text embeddings $tp$ as pivots/prototypes, and map TS embeddings to them. In the code, the prototypes were found using KMeans. Then the alignment is found using the feature-wise constrast:
$$ \begin{aligned} \mathcal{L}{text} = -\sum{i=1}^P \sigma(tp_i,e) - \mathcal{L}_{fea}(e\cdot tp_i, e^+ \cdot tp_i, e^- \cdot tp_i) \end{aligned} $$
The overall contrastive loss is in the contrastive_loss.py file.
# in contrastive_loss.py
# positives
if self.text_prototype == False:
loss = -torch.mean(torch.nn.functional.logsigmoid(torch.bmm(
representation.view(batch_size, 1, size_representation),
positive_representation.view(batch_size, size_representation, 1)
)))
else:
save_memory = False
loss = -torch.mean(torch.nn.functional.logsigmoid(torch.bmm(
representation.view(batch_size, 1, size_representation),
positive_representation.view(batch_size, size_representation, 1)
)) + torch.nn.functional.logsigmoid(torch.bmm(
representation.view(batch_size, 1, size_representation),
self.text_prototype.view(batch_size, size_representation, 1)))
for i in range(self.nb_random_samples):
# Negative loss: -logsigmoid of minus the dot product between
# anchor and negative representations
negative_representation = encoder(
torch.cat([train[samples[i, j]: samples[i, j] + 1][
:, :,
beginning_samples_neg[i, j]:
beginning_samples_neg[i, j] + length_pos_neg
] for j in range(batch_size)])
)
loss += multiplicative_ratio * -torch.mean(
torch.nn.functional.logsigmoid(-torch.bmm(
representation.view(batch_size, 1, size_representation),
negative_representation.view(
batch_size, size_representation, 1
)
))
)
Soft Prompting

Soft prompting is a technique that concatenates learnable embeddings to the input of a LLM, which is usually tailor made for a specific task. There are several ways to apply soft prompting, and TEST uses the technique of P-tuning , which uses a LSTM encoder to optimize prompt parameters. However, not very clear how this is implemented in the code.
Conclusion
This paper presented a different way to encode and align time series and to be used with LLM. However, the writing style is not very clear, and the codebase is not very straight forward either. On top of that, the performance is not as good as TimeLLM. Still, it is an interesting approach, and the method of contrastive learning can be further explored in this line of work that aligns the embedding spaces of time series and text.