Time series forecasting has been a hot topic in the field of deep learning, and there are many interesting models proposed in the last few years. TimeLLM is a novel approach that integrates temporal information into the LLM training process, and it is a very interesting approach. In this post, I will link the paper’s content with the code, and discuss the implementation details. This is helpful for me since I plan to use LLM for time series forecasting in the future. Without further ado, we directly dive into the design choices and the corresponding implementation in the code.
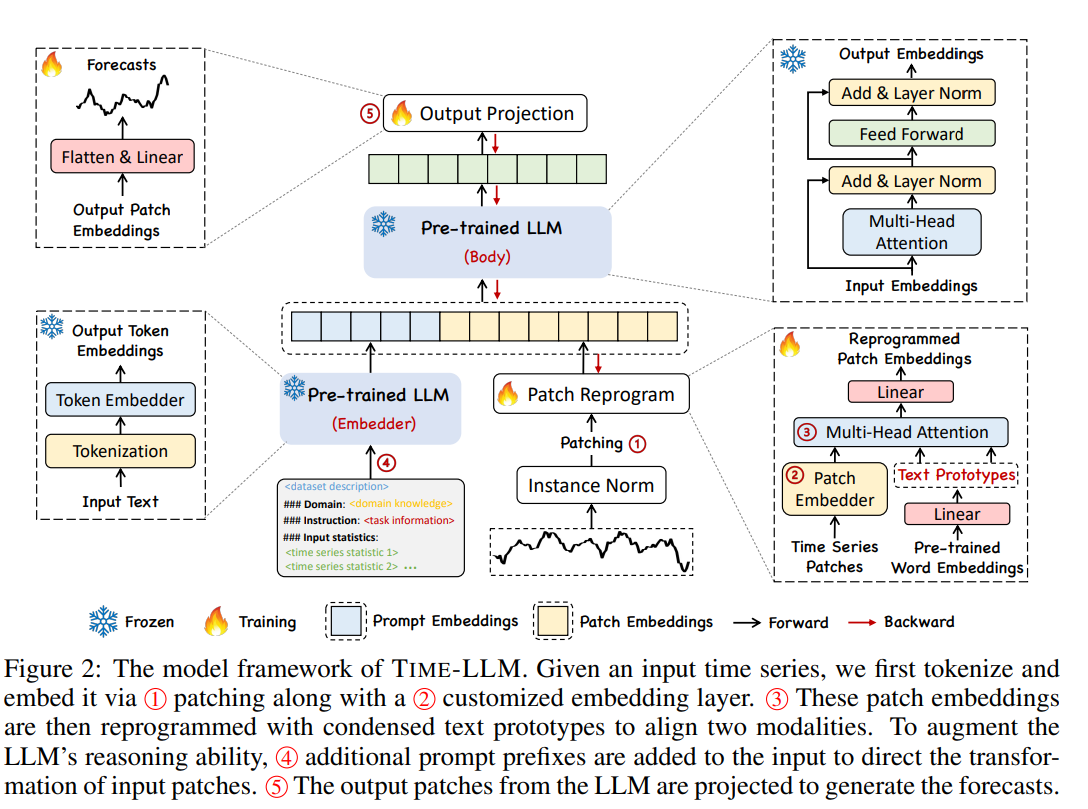
We follow the standard analysis process by first looking at the input data and the overall forward pass architecture. The inputs are prompts and patches of time series data (they termed it as “patches” because the time series data are divided into small segments). The forward pass architecture is shown in the figure above.
Input Formulation (Prompting and Patching)
Q1: What is the input to the model’s forward pass?
In the module models.TimeLLM.py and in the run_main.py file, we can see the following code snippet:
# in models.TimeLLM.py
def forward(self, x_enc, x_mark_enc, x_dec, x_mark_dec, mask=None):
if self.task_name == 'long_term_forecast' or self.task_name == 'short_term_forecast':
dec_out = self.forecast(x_enc, x_mark_enc, x_dec, x_mark_dec)
return dec_out[:, -self.pred_len:, :]
return None
def forecast(self, x_enc, x_mark_enc, x_dec, x_mark_dec):
# ignore
# in run_main.py
outputs = model(batch_x, batch_x_mark, dec_inp, batch_y_mark)
where the batch_x is the input time series data, batch_x_mark is the time stamp, dec_inp is the decoder input, and batch_y_mark is the time stamp for the decoder input, which we can check from the data_provider.data_loader.py file.
# in the scope of the dataloader.
df_stamp['month'] = df_stamp.date.apply(lambda row: row.month, 1)
df_stamp['day'] = df_stamp.date.apply(lambda row: row.day, 1)
df_stamp['weekday'] = df_stamp.date.apply(lambda row: row.weekday(), 1)
df_stamp['hour'] = df_stamp.date.apply(lambda row: row.hour, 1)
data_stamp = df_stamp.drop(['date'], 1).values
# in data_provider.data_loader.py
def __getitem__(self, index):
feat_id = index // self.tot_len
s_begin = index % self.tot_len
s_end = s_begin + self.seq_len
r_begin = s_end - self.label_len
r_end = r_begin + self.label_len + self.pred_len
seq_x = self.data_x[s_begin:s_end, feat_id:feat_id + 1]
seq_y = self.data_y[r_begin:r_end, feat_id:feat_id + 1]
seq_x_mark = self.data_stamp[s_begin:s_end]
seq_y_mark = self.data_stamp[r_begin:r_end]
return seq_x, seq_y, seq_x_mark, seq_y_mark
However, it seems that in the model class, the timestamps were not used. Instead, x_enc, the encoder input, is used to calculate a number of statistics (min, max, median, lags) and the results are used as part of the prompt for the LLM, as shown in the following code snippet:
# in models.TimeLLM.py
def forecast(self, x_enc, x_mark_enc, x_dec, x_mark_dec):
# ignore
min_values_str = str(min_values[b].tolist()[0])
max_values_str = str(max_values[b].tolist()[0])
median_values_str = str(medians[b].tolist()[0])
lags_values_str = str(lags[b].tolist())
prompt_ = (
f"<|start_prompt|>Dataset description: {self.description}"
f"Task description: forecast the next {str(self.pred_len)} steps given the previous {str(self.seq_len)} steps information; "
"Input statistics: "
f"min value {min_values_str}, "
f"max value {max_values_str}, "
f"median value {median_values_str}, "
f"the trend of input is {'upward' if trends[b] > 0 else 'downward'}, "
f"top 5 lags are : {lags_values_str}<|<end_prompt>|>"
)
prompt = self.tokenizer(prompt, return_tensors="pt", padding=True, truncation=True, max_length=2048).input_ids
prompt_embeddings = self.llm_model.get_input_embeddings()(prompt.to(x_enc.device)) # (batch, prompt_token, dim)
The components of the prompt are:
- Dataset description: a description of the dataset, which is provided by the user.
- Task description: the task to be performed, which is “forecast the next $L$ steps given the previous $L$ steps information”.
- Input statistics: some statistics of the input time series, including the minimum, maximum, median, and the trend of the input.
- Top 5 lags: the top 5 lags of the input time series.
Hence to answer Q1, the input to the model’s forward pass is the encoder input x_enc, the time stamp for the encoder input x_mark_enc, the decoder input x_dec, and the time stamp for the decoder input x_mark_dec, and the intermediate results are the statistics and the corresponding prompts.
Multi-Modal Alignment
Crucial to this paper’s central theme is the notion of LLM reprogramming, where the time series is splitted into patches, and then, together with the embedding of the prompts, is aligned with the LLM’s word embeddings. Here we ask:
Q2: What are the steps of LLM reprogramming?
Let the time series be denoted by $X$ and each dimension $X^{(i)}$. From the paper, we see the following steps:
- Input Embedding: each input channel is $X^{(i)}$:
- normalized using reversible instance normalization (RevIN)
- divided into patches, resulting in $X^{(i)}_P \in \mathbb{R}^{P \times L_P}$, where $P$ is the number of patches and $L_P$ is the length of each patch.
- use a linear layer to embed each patch into a vector, resulting in $\hat{X}^{(i)}_P \in \mathbb{R}^{P \times d_m}$, where $d_m$ is the dimension of the embedding space.
The following code snippet shows the implementation of the input embedding:
# normalize layer is the RevIN in layers.StandardNorm.py
x_enc = self.normalize_layers(x_enc, 'norm')
x_enc = x_enc.permute(0, 2, 1).contiguous().reshape(B * N, T, 1)
x_enc = x_enc.permute(0, 2, 1).contiguous()
# patch_embedding in layers.Embed.py
enc_out, n_vars = self.patch_embedding(x_enc.to(torch.bfloat16))
- Patch Reprogramming:
After encoding the patches, they attempt to bridge the gap between the patch embeddings and the LLM’s word embeddings. They first think about using attention to align the patch embeddings and the LLM’s word embeddings, but they find that the attention is too expensive to compute. They then try to probe the word embedding and only use a subset of words to do so (called “patch reprogramming”). This is implemented as a simple linear layer.
# mapping_layer gets the subset of word embeddings
self.mapping_layer = nn.Linear(self.vocab_size, self.num_tokens)
source_embeddings = self.mapping_layer(self.word_embeddings.permute(1, 0)).permute(1, 0)
- Cross-Modality Alignment:
Now they combine the patch embeddings with the source embeddings (subset of word embeddings) using a ReprogrammingLayer, which is implemented as multiheaded attention.
$$ Z_k^{(i)} = \text{Attention}(Q_k^{(i)}, K_k^{(i)}, V_k^{(i)}) = \text{softmax}\left(\frac{Q_k^{(i)} K_k^{(i)T}}{\sqrt{d_k}}\right) V_k^{(i)} $$
where $Q_k^{(i)} = \text{Linear}(enc_out)$, $K_k^{(i)} = \text{Linear}(source_embeddings)$, and $V_k^{(i)} = source_embeddings$. The following code snippet shows the implementation of the cross-modality alignment:
self.vocab_size = self.word_embeddings.shape[0]
self.num_tokens = 1000
self.mapping_layer = nn.Linear(self.vocab_size, self.num_tokens)
source_embeddings = self.mapping_layer(self.word_embeddings.permute(1, 0)).permute(1, 0)
enc_out, n_vars = self.patch_embedding(x_enc.to(torch.bfloat16))
enc_out = self.reprogramming_layer(enc_out, source_embeddings, source_embeddings)
self.reprogramming_layer = ReprogrammingLayer(configs.d_model, configs.n_heads, self.d_ff, self.d_llm)
# in TimeLLM.py
class ReprogrammingLayer(nn.Module):
def __init__(self, d_model, n_heads, d_keys=None, d_llm=None, attention_dropout=0.1):
super(ReprogrammingLayer, self).__init__()
d_keys = d_keys or (d_model // n_heads)
self.query_projection = nn.Linear(d_model, d_keys * n_heads)
self.key_projection = nn.Linear(d_llm, d_keys * n_heads)
self.value_projection = nn.Linear(d_llm, d_keys * n_heads)
self.out_projection = nn.Linear(d_keys * n_heads, d_llm)
self.n_heads = n_heads
self.dropout = nn.Dropout(attention_dropout)
def forward(self, target_embedding, source_embedding, value_embedding):
B, L, _ = target_embedding.shape
S, _ = source_embedding.shape
H = self.n_heads
target_embedding = self.query_projection(target_embedding).view(B, L, H, -1)
source_embedding = self.key_projection(source_embedding).view(S, H, -1)
value_embedding = self.value_projection(value_embedding).view(S, H, -1)
out = self.reprogramming(target_embedding, source_embedding, value_embedding)
out = out.reshape(B, L, -1)
return self.out_projection(out)
def reprogramming(self, target_embedding, source_embedding, value_embedding):
B, L, H, E = target_embedding.shape
scale = 1. / sqrt(E)
scores = torch.einsum("blhe,she->bhls", target_embedding, source_embedding)
A = self.dropout(torch.softmax(scale * scores, dim=-1))
reprogramming_embedding = torch.einsum("bhls,she->blhe", A, value_embedding)
return reprogramming_embedding
The output dimension of the reprogramming layer is the same as the dimension of LLM’s word embeddings.
Prompt-as-Prefix and Forecasting
In the paper, they claim that prompt embedding can be used as prefix for the patch embeddings of the time series. In this case, the LLM’s decoder is used to convert the concatenated patch embeddings and the prompt embeddings into a hidden representation, which is then used to forecast the future values of the time series. The following code snippet shows the implementation of the prompt-as-prefix and forecasting:
# in models.TimeLLM.forecast
llama_enc_out = torch.cat([prompt_embeddings, enc_out], dim=1)
dec_out = self.llm_model(inputs_embeds=llama_enc_out).last_hidden_state
dec_out = dec_out[:, :, :self.d_ff]
dec_out = torch.reshape(
dec_out, (-1, n_vars, dec_out.shape[-2], dec_out.shape[-1]))
dec_out = dec_out.permute(0, 1, 3, 2).contiguous()
dec_out = self.output_projection(dec_out[:, :, :, -self.patch_nums:])
dec_out = dec_out.permute(0, 2, 1).contiguous()
dec_out = self.normalize_layers(dec_out, 'denorm')
return dec_out
LLM in Constructor
The model offers a number of choices of LLMs. The following code snippet shows the implementation of the LLM in the constructor:
- LLAMA7B
- GPT2
- BERT
Here we take a look at only the LLAMA7B case.
if configs.llm_model == 'LLAMA':
# self.llama_config = LlamaConfig.from_pretrained('/mnt/alps/modelhub/pretrained_model/LLaMA/7B_hf/')
self.llama_config = LlamaConfig.from_pretrained('huggyllama/llama-7b')
self.llama_config.num_hidden_layers = configs.llm_layers
self.llama_config.output_attentions = True
self.llama_config.output_hidden_states = True
self.llm_model = LlamaModel.from_pretrained(
# "/mnt/alps/modelhub/pretrained_model/LLaMA/7B_hf/",
'huggyllama/llama-7b',
trust_remote_code=True,
local_files_only=True,
config=self.llama_config,
load_in_8bit=True
)
self.tokenizer = LlamaTokenizer.from_pretrained(
# "/mnt/alps/modelhub/pretrained_model/LLaMA/7B_hf/tokenizer.model",
'huggyllama/llama-7b',
trust_remote_code=True,
local_files_only=True
)
# freeze the LLM parameters
for param in self.llm_model.parameters():
param.requires_grad = False
Conclusion
The implementation flow of TimeLLM is interesting and also quite straightforward. The paper’s central theme is the notion of LLM reprogramming, where the time series is splitted into patches, and then, together with the embedding of the prompts, is aligned with the LLM’s word embeddings. The concatenation of the prompt embeddings and the patch embeddings are then used by the decoder of the LLM to be used as state for final forecasting. The paper is a very interesting read and the implementation is something that can be used as a template for future works in this direction.